" Τα μαθηματικά είναι ένα όμορφο και απολαυστικό παιχνίδι. Aπλά έχει δύσκολους κανόνες παιχνιδιού".
Τα καθαρά Μαθηματικά είναι το καλύτερο παιχνίδι του κόσμου. Σε καθηλώνει πιο πολύ από το σκάκι, έχει μεγαλύτερο ρίσκο από το πόκερ και διαρκεί περισσότερο από τη Μονόπολη. Και είναι δωρεάν, μπορείς να το παίξεις παντού -ο Αρχιμήδης το έπαιζε στη μπανιέρα του.
Richard J. Trudeau
Επιπλέον βέβαια προβλήματα , σπαζοκεφαλιές μπορείτε να βρείτε και στην ανάρτησή μας : "ΧΑΡΤΙ ΚΑΙ ΜΟΛΥΒΙ : Η ΑΣΚΗΣΗ ΤΗΣ ΗΜΕΡΑΣ ".
Λεονάρντο Ντα Βίντσι.
1. ΓΕΩΜΕΤΡΙΚΗ ΨΕΥΔΑΙΣΘΗΣΗ

Γιατί στράβωσε το συρματόπλεγμα; Ή μήπως όχι.
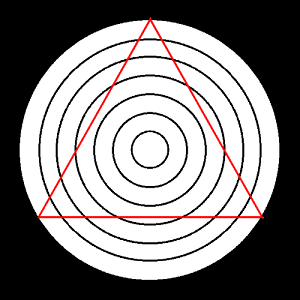
Οι πλευρές του τριγώνου μοιάζουν σαν να έχουν στραβώσει.

Ποια από τις δύο κατακόρυφες γραμμές είναι μακρύτερη; Ή μήπως είναι ίσες;

Κι όμως τα ευθύγραμμα τμήματα είναι ίσα.

Μπορείτε να μετρήσετε τις μαύρες κουκκίδες;

Βλέπετε τους κύκλους; Στην πραγματικότητα δεν υπάρχουν.

Μία μόνο απόχρωση του πράσινου υπάρχει!

Βλέπετε ένα σπιράλ; Κι όμως πρόκειται για ανεξάρτητους κύκλους.
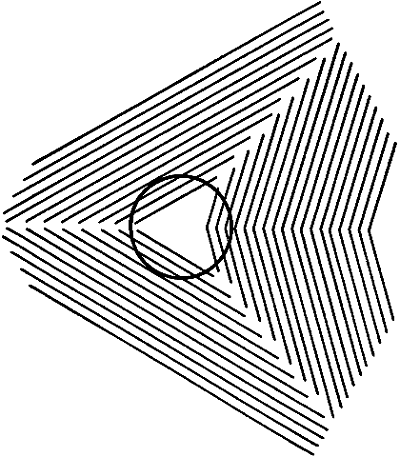
Νομίζετε ότι στράβωσε ο κύκλος; Νομίζετε…
Πολλές από αυτές τις οφθαλμαπάτες αλλά και άλλες μπορείτε να βρείτε εδώ
ΔΙΦΟΡΟΥΜΕΝΕΣ ΕΙΚΟΝΕΣ
Multistability, αντίληψη multistable ή κάποιες φορές αποδιδόμενη στα ελληνικά «δισταθής αντίληψη» είναι το φαινόμενο κατά το οποίο o ανθρώπινος εγκέφαλος μπορεί να έχει διφορούμενες, εναλλασσόμενες προσλήψεις ή εντυπώσεις από μία σταθερή εικόνα.
Περίφημο παράδειγμα που περιλαμβάνεται σε πολλά εγχειρίδια τέχνης είναι το «βάζο του Rubin». Η εικόνα, μία από ένα σετ πολυμορφικών εικόνων που δημιούργησε το 1915 ο δανός ψυχολόγος Edgar Rubin για να εξηγήσει τους μηχανισμούς πολλαπλής πρόσληψης από τον εγκέφαλο, παρουσιάζει ένα οπτικό παιχνίδι διπλής εικόνας. Ο θεατής μπορεί να δει είτε ένα βάζο στο κέντρο της εικόνας είτε την παρουσία δύο ανθρώπινων προφίλ που σχηματίζονται δεξιά και αριστερά από το κεντρικό περίγραμμα του βάζου.
ΠΡΟΣΩΠΑ Η ΚΥΠΕΛΟ;
ΟΙ ΔΙΠΛΟΙ ΕΦΙΠΠΟΙ
![[hrsmn.jpg]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgcS653lvJs5phMRiAjYppICVZc-ZDWF36h98xahPy3RQg4DQKk8ITTlcoZKKKLXQimv4QBWoEd-2PYmFTJHSbthWqjR1u5mnk8ZI5ya2DsYA9TqltOQwrWWo3F2L48z_-ZO2QV54I7fFU/s200/hrsmn.jpg)
ΙΝΔΙΑΝΟΣ Η ΕΣΚΙΜΩΟΣ;
ΑΔΥΝΑΤΑ ΑΝΤΙΚΕΙΜΕΝΑ
Είναι δυνατόν να βλέπουμε κάτι άλλο από αυτό που υπάρχει πραγματικά;Υπάρχει τρόπος να εξαπατηθούν τα μάτια μας; Ή ο εγκέφαλός μας; Ο κόσμος της οφθαλμαπάτης έχει αμφισβητηθεί πολλές φορές, αποτελεί όμως ένα ευχάριστο παιχνίδι του μυαλού.
Διάβαζε και ας σου φανεί παράξενο.
Σωφνυμα με μετελη Αγκιλγου Πεπανησιμοτυ η σριεα των γωραματμν σε μια λξεη δεν εεχι σαιμησα ατυο που μρετα εαινι το πωτρο και το τλευτιαεο γμαρμα. Τα υλιοποπα μοπορυν να εαινι σε οηπιδτοε σριεα και μεριπος αοκμα να δαεζιαβις χριως πβηρλμοα.
Ο ψυχίατρος κος Θ. Δασκαλόπουλος αναφέρει: “φαίνεται πως ο οφθαλμός από την οπτική σάρωση του κειμένου , μεταδίδει στον εγκέφαλο , ολόκληρα πακέτα πληροφορίας για κάθε λέξη και όχι για κάθε γράμμα ξεχωριστά.”
Δείτε για παράδειγμα την παρακάτω λέξη:
τλευτιαεο
David Hilbert ( 1862 - 1943 ).
Τα καθαρά Μαθηματικά είναι το καλύτερο παιχνίδι του κόσμου. Σε καθηλώνει πιο πολύ από το σκάκι, έχει μεγαλύτερο ρίσκο από το πόκερ και διαρκεί περισσότερο από τη Μονόπολη. Και είναι δωρεάν, μπορείς να το παίξεις παντού -ο Αρχιμήδης το έπαιζε στη μπανιέρα του.
Richard J. Trudeau
Εδώ περιέχονται μαθηματικοί γρίφοι , σπαζοκεφαλιές , παιχνίδια , αινίγματα ,έξυπνες κατασκευές , μαγικά τετράγωνα , σταυρόλεξα , sudoku, γεωμετρικές οφθαλμαπάτες , παράδοξα κ.α. Αναδεικνύεται έτσι η διασκεδαστική και ψυχαγωγική όψη των μαθηματικών που μπορούν να γεμίσουν ευχάριστα τον ελεύθερο χρόνο μας.
Επιπλέον βέβαια προβλήματα , σπαζοκεφαλιές μπορείτε να βρείτε και στην ανάρτησή μας : "ΧΑΡΤΙ ΚΑΙ ΜΟΛΥΒΙ : Η ΑΣΚΗΣΗ ΤΗΣ ΗΜΕΡΑΣ ".
Ο ΜΑΓΙΚΟΣ ΚΟΣΜΟΣ ΤΩΝ ΟΦΘΑΛΜΑΠΑΤΩΝ
" Κάποιοι βλέπουν , κάποιοι βλέπουν μόνο αν τους δείξει κάποιος κάτι να δουν και κάποιοι δεν βλέπουν".
Λεονάρντο Ντα Βίντσι.
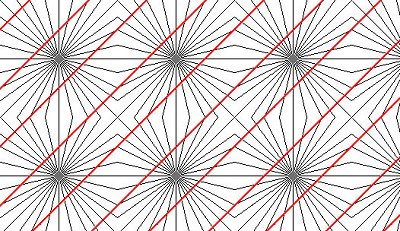
Οι κόκκινες γραμμές είναι ευθείες ή καμπύλες ; κι όμως είναι ευθείες. Διαπιστώθηκε ότι όταν ακτινωτές γραμμές περιβάλλονται από παράλληλες ευθείες , οι τελευταίες φαίνονται ως καμπύλες.
Παρόμοια ψευδαίσθηση και η παρακάτω :

2. Γεωμετρικές Πλάνες

Γιατί στράβωσε το συρματόπλεγμα; Ή μήπως όχι.

Οι πλευρές του τριγώνου μοιάζουν σαν να έχουν στραβώσει.

Ποια από τις δύο κατακόρυφες γραμμές είναι μακρύτερη; Ή μήπως είναι ίσες;

Κι όμως τα ευθύγραμμα τμήματα είναι ίσα.

Μπορείτε να μετρήσετε τις μαύρες κουκκίδες;

Βλέπετε τους κύκλους; Στην πραγματικότητα δεν υπάρχουν.

Μία μόνο απόχρωση του πράσινου υπάρχει!

Βλέπετε ένα σπιράλ; Κι όμως πρόκειται για ανεξάρτητους κύκλους.

Νομίζετε ότι στράβωσε ο κύκλος; Νομίζετε…
Πολλές από αυτές τις οφθαλμαπάτες αλλά και άλλες μπορείτε να βρείτε εδώ
3. ΠΡΟΣΕΞΤΕ ΤΑ ΠΑΡΑΚΑΤΩ ΠΑΡΑΔΟΞΑ.
ΔΙΦΟΡΟΥΜΕΝΕΣ ΕΙΚΟΝΕΣ
Multistability, αντίληψη multistable ή κάποιες φορές αποδιδόμενη στα ελληνικά «δισταθής αντίληψη» είναι το φαινόμενο κατά το οποίο o ανθρώπινος εγκέφαλος μπορεί να έχει διφορούμενες, εναλλασσόμενες προσλήψεις ή εντυπώσεις από μία σταθερή εικόνα.
Περίφημο παράδειγμα που περιλαμβάνεται σε πολλά εγχειρίδια τέχνης είναι το «βάζο του Rubin». Η εικόνα, μία από ένα σετ πολυμορφικών εικόνων που δημιούργησε το 1915 ο δανός ψυχολόγος Edgar Rubin για να εξηγήσει τους μηχανισμούς πολλαπλής πρόσληψης από τον εγκέφαλο, παρουσιάζει ένα οπτικό παιχνίδι διπλής εικόνας. Ο θεατής μπορεί να δει είτε ένα βάζο στο κέντρο της εικόνας είτε την παρουσία δύο ανθρώπινων προφίλ που σχηματίζονται δεξιά και αριστερά από το κεντρικό περίγραμμα του βάζου.
ΠΡΟΣΩΠΑ Η ΚΥΠΕΛΟ;
ΟΙ ΔΙΠΛΟΙ ΕΦΙΠΠΟΙ
![[hrsmn.jpg]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgcS653lvJs5phMRiAjYppICVZc-ZDWF36h98xahPy3RQg4DQKk8ITTlcoZKKKLXQimv4QBWoEd-2PYmFTJHSbthWqjR1u5mnk8ZI5ya2DsYA9TqltOQwrWWo3F2L48z_-ZO2QV54I7fFU/s200/hrsmn.jpg)
ΙΝΔΙΑΝΟΣ Η ΕΣΚΙΜΩΟΣ;
ΑΔΥΝΑΤΑ ΑΝΤΙΚΕΙΜΕΝΑ
Είναι δυνατόν να βλέπουμε κάτι άλλο από αυτό που υπάρχει πραγματικά;Υπάρχει τρόπος να εξαπατηθούν τα μάτια μας; Ή ο εγκέφαλός μας; Ο κόσμος της οφθαλμαπάτης έχει αμφισβητηθεί πολλές φορές, αποτελεί όμως ένα ευχάριστο παιχνίδι του μυαλού.
Διάβαζε και ας σου φανεί παράξενο.
Σωφνυμα με μετελη Αγκιλγου Πεπανησιμοτυ η σριεα των γωραματμν σε μια λξεη δεν εεχι σαιμησα ατυο που μρετα εαινι το πωτρο και το τλευτιαεο γμαρμα. Τα υλιοποπα μοπορυν να εαινι σε οηπιδτοε σριεα και μεριπος αοκμα να δαεζιαβις χριως πβηρλμοα.
Ο ψυχίατρος κος Θ. Δασκαλόπουλος αναφέρει: “φαίνεται πως ο οφθαλμός από την οπτική σάρωση του κειμένου , μεταδίδει στον εγκέφαλο , ολόκληρα πακέτα πληροφορίας για κάθε λέξη και όχι για κάθε γράμμα ξεχωριστά.”
Δείτε για παράδειγμα την παρακάτω λέξη:
τλευτιαεο
Δύσκολα αντιλαμβάνεται κανείς τι σημαίνει. Παρόλο που χωρίς δυσκολίες την διαβάσατε πριν στο κείμενο, έξω από αυτό και μόνη της , δεν γίνεται αντιληπτή. Τα συμφραζόμενα είναι που δίνουν την κατανόηση.
Πράγματι υπάρχουν πολλές γλώσσες και σήμερα , που αφήνουν τα σύμβολα του γραπτού λόγου να ταιριάζουν , μέσα στο νου μας , στη σωστή έννοια.
α) Αντικείμενα που δεν υπάρχουν
Τα αδύνατα σχήματα είναι η αγαπημένη κατηγορία των ζωγράφων. Τα σχέδια ξεφεύγουν από την πραγματικότητα και μας οδηγούν σε ανύπαρκτους κόσμους. Ο Oscar Rentersvard θεωρείται ο πατέρας των αδύνατων σχημάτων. Έχει δημιουργήσει κατά τη διάρκεια της ζωής του χιλιάδες τέτοια σχήματα , όπως το αδύνατο τρίγωνο , η αδύνατη σκάλα κ.α.
![[LW439.jpg]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgWLH9TJygcr2GWh88rIFMNTplVfgX-Vk31-y2EF20xTGD35yzV3QyQOmNCwcDguPGFhDIPlPIvHlV_3sjr0bKdKQHWw5OtJv0M_rRCx34Qej6lYqymAddw1OFBrIqOumnzI1gL5esTP30/s320/LW439.jpg)
O "Καταρράκτης" του Μάοριτς Κορνέλις Έσερ είναι ένα σκίτσο που δείχνει ένα κανάλι νερού που οδηγείται σε ένα μικρό καταρράκτη. Το νερό πέφτει σε ένα νερόμυλο που βρίσκεται στο επίπεδο από όπου ξεκινά το κανάλι. Όπως καταλαβαίνεις, είναι μια εικόνα αδύνατη, να την κοιτάς και να ζαλίζεσαι, όπως όλες οι εικόνες του Έσερ που έχεις δει κρεμασμένες σε τοίχους φοιτητικών δωματίων.

Η ταινία Μέμπιους είναι μια επιφάνεια που έχει μόνο μία πλευρά αλλά είναι δυνατόν να τη διατρέξει κανείς σε όλο της το μήκος έχοντας την αίσθηση ότι αλλάζει μεριά (κάτι που γίνεται εμφανές και στο σχέδιο του Escher – τα μυρμήγκια βοηθούν σε αυτό). Εύκολα μπορεί κάποιος να φτιάξει αυτό το σχήμα ακόμη και με ένα μακρύ κομμάτι χαρτί του οποίου θα περιστρέψει το ένα άκρο κατά 180 μοίρες και ύστερα θα ενώσει τις άκρες του φτιάχνοντας ένα ενιαίο, συνεχές κομμάτι. Δεν είναι τυχαίο που το σχήμα της ταινίας του Μέμπιους θυμίζει το μαθηματικό σύμβολο του απείρου. Τα μυρμήγκια της εικόνας θα μπορούσαν να προχωρούν για πάντα και να παρέμεναν μονίμως στην ίδια μεριά.
ΕΝΑ ΠΑΝΑΡΧΑΙΟ ΚΙΝΕΖΙΚΟ ΠΑΙΧΝΙΔΙ
ΓΕΩΜΕΤΡΙΚΟΥ ΠΑΖΛ.
( ΔΕΝ ΕΙΝΑΙ ΟΦΘΑΛΜΑΠΑΤΗ )
Tangram...
• Ένα μεσαίο ορθογώνιο και ισοσκελές τρίγωνο.
• Δύο μικρά ορθογώνια και ισοσκελή τρίγωνα.
• Ένα τετράγωνο.
• Και ένα πλάγιο παραλληλόγραμμο.
Με αυτά τα 7 γεωμετρικά σχήματα προσπαθήστε να φτιάξετε τα αντικείμενα που βλέπεται παρακάτω. Κανόνας του παιχνιδιού είναι τα κομμάτια να τοποθετούνται το ένα δίπλα στο άλλο ώστε να εφάπτονται οι πλευρές τους και όχι το ένα να καλύπτει μέρος του άλλου.
Ορισμός του προβλήματος…
Οποιαδόποτε επιφάνεια που χωρίζεται σε περιοχές, όπως ένας πολιτικός χάρτης των νομών ενός κράτους, μπορούν να χρωματιστούν χρησιμοποιώντας λιγότερα από τέσσερα χρώματα κατά τέτοιο τρόπο ώστε καμία από δύο παρακείμενες περιοχές να μην έχουν το ίδιο χρώμα. ήταν το πρώτο σημαντικό θεώρημα που αποδεικνύεται, χρησιμοποιώντας υπολογιστή, και η απόδειξη δεν είναι αποδεκτή από όλους τους μαθηματικούς επειδή θα ήταν αδύνατον για έναν άνθρωπο να το ελέγξει με το χέρι.
Ιστορικά…
Η υπόθεση προτάθηκε αρχικά το 1852, όταν ο φοιτητής Francis Guthrie προσπαθούσε να χρωματίσει το χάρτη των περιφερειών της Αγγλίας.Στα 1976 το θεώρημα των 4 χρωμάτων αποδείχθηκε τελικά από τον Kenneth Appel και Wolfgang Haken από το πανεπιστήμιο του Ιλλινόις . Βοηθήθηκαν από τον John Koch και τον υπολογιστή του (επί 1200 ώρες).
ΤΟ ΘΕΩΡΗΜΑ ΤΗΣ ΠΙΤΣΑΣ.

MAΘΗΜΑΤΙΚΑ ΠΑΡΑΔΟΞΑ
1. Ο Αχιλλέας και η χελώνα ( παράδοξο του Ζήνωνα).
Ο Ζήνωνας, αρχαίος Έλληνας μαθηματικός και φιλόσοφος, είχε θέσει κάποια μαθηματικά παράδοξα που ταλαιπώρησαν τους μαθηματικούς των επόμενων αιώνων στην προσπάθειά τους να δώσουν μια «επιστημονικά σωστή» λύση.
Όπως για παράδειγμα το παράδοξο του Αχιλλέα με τη χελώνα που τρέχουν σ' ένα δρόμο ταχύτητας. Ο Ζήνωνας υποστήριξε ότι, ποτέ ο Αχιλλέας δεν θα καταφέρει να ξεπεράσει την προπορευόμενη χελώνα! Kάθε φορά που o Aχιλλέας θα φτάνει στο σημείο που βρίσκονταν πριν από λίγο η χελώνα, αυτή θα έχει ήδη προχωρήσει (έστω και) λίγο πιο μπροστά… Έτσι αν και ο γοργοπόδαρος Αχιλλέας θα μειώνει συνεχώς την απόσταση απ' την προπορευόμενη χελώνα, ποτέ δεν θα την ξεπεράσει!!!
Παράδοξο που οδηγεί στον απειροστικό λογισμό, όπως και ένα παρόμοιό του, σύμφωνα με το οποίο, ούτε ο Αχιλλέας, αλλά ούτε και η χελώνα θα τερματίσουν ποτέ! Γιατί;
Για να τερματίσουν θα πρέπει πρώτα να φτάσουν στο μέσο της διαδρομής. Όταν φτάσουν στο μέσο θα πρέπει να διανύσουν το πρώτο μισό του εναπομείναντος διαστήματος. Και φυσικά όταν θα το κάνουν αυτό θα πρέπει και πάλι να διανύσουν το επόμενο πρώτο μισό. Και αυτό θα συνεχίζεται επ' άπειρον.
Κι άλλα παράδοξα του Ζήνωνα : εδώ
2. Παράδοξο του κουρέα (παράδοξο του Ράσσελ).
1η διατύπωση
Διατυπώνεται ως εξής: “Σε μια χώρα που όλοι οι άντρες είναι καθημερινά ξυρισμένοι, υπάρχει ένας μόνο κουρέας. Αυτός ξυρίζει όλους τους άντρες που δεν ξυρίζονται μόνοι τους. Τότε όμως ποιος ξυρίζει τον κουρέα;”. Αναλύοντας το πρόβλημα με τη βοήθεια της Θεωρίας των Συνόλων, είναι σαφές ότι στη χώρα υπάρχουν το σύνολο εκείνων που ξυρίζονται μόνοι τους και το σύνολο εκείνων που ξυρίζονται στον κουρέα. Ο κουρέας ξυρίζεται μόνος του;
Αδύνατον, αφού ξυρίζει όλους τους άντρες που δεν ξυρίζονται μόνοι τους. Τον ξυρίζει κάποιος άλλος; Όχι, γιατί ο κουρέας ξυρίζει όλους όσοι δεν ξυρίζονται μόνοι τους. Βρισκόμαστε εδώ μπροστά σ’ ένα παράδοξο. Σύμφωνα με τον Ράσελ, για να το ξεπεράσουμε πρέπει να διορθώσουμε τη δική μας λανθασμένη αντίληψη ότι για κάθε ιδιότητα πρέπει οπωσδήποτε να υπάρχει ένα σύνολο. Σ’ αυτή την περίπτωση δε δημιουργείται κανένα ομοιογενές σύνολο.
2η διατύπωση
Σε ένα χωριό όπου υπάρχει ένας κουρέας οι μισοί άντρες ξυρίζονται στον κουρέα και οι άλλοι μισοί ξυρίζονται μόνοι τους . Ο κουρέας σε ποιά από τις δύο ομάδες ανήκει , σε αυτούς που ξυρίζονται μόνοι τους ή σε αυτούς που τους ξυρίζει ο κουρέας;
3. Το παράδοξο των αλόγων ( όλα τα άλογα έχουν το ίδιο χρώμα)
Υποθέστε ότι έχουμε ένα σύνολο 5 αλόγων. Επιθυμούμε να αποδείξουμε ότι είναι όλο το ίδιο χρώμα. Υποθέστε ότι είχαμε μια απόδειξη ότι όλα τα σύνολα 4 αλόγων ήταν το ίδιο χρώμα. Εάν αυτός ίσχυε, θα μπορούσαμε να αποδείξουμε ότι και τα πέντε άλογα είναι το ίδιο χρώμα με τη διαίρεση των αλόγων σε δύο επικαλύπτοντας ομάδες τεσσάρων αλόγων κάθε ένα. Από την υποτιθέμενη υπάρχουσα απόδειξή μας, δεδομένου ότι αυτές είναι ομάδες 4, όλα τα άλογα σε τα πρέπει να είναι το ίδιο χρώμα. Παραδείγματος χάριν, ο πρώτος, το δευτερόλεπτο, τρίτα και τέταρτα τα άλογα αποτελούν μια ομάδα τεσσάρων, και πρέπει έτσι όλα να είναι το ίδιο χρώμα και τα δεύτερα, τρίτα, τέταρτα και πέμπτα άλογα αποτελούν επίσης μια ομάδα τεσσάρων και πρέπει έτσι επίσης όλα να είναι το ίδιο χρώμα. Για αυτό για να εμφανιστεί, και τα πέντε άλογα στην ομάδα των 5 πρέπει να είναι το ίδιο χρώμα.
Αλλά πώς είμαστε για να πάρουμε μια απόδειξη ότι όλα τα σύνολα 4 αλόγων είναι το ίδιο χρώμα; Εφαρμόζουμε την ίδια λογική πάλι. Με την ίδια διαδικασία, μια ομάδα 4 αλόγων θα μπορούσε να αναλυθεί στις ομάδες 3, και έπειτα μια ομάδα 3 αλόγων θα μπορούσε να αναλυθεί στις ομάδες 2, et ainsi de suite και τα λοιπά. Τελικά θα φθάσουμε σε ένα μέγεθος ομάδας 1, και είναι προφανές ότι όλα τα άλογα σε μια ομάδα 1 αλόγου πρέπει να είναι το ίδιο χρώμα.
Από την ίδια λογική μπορούμε επίσης να αυξήσουμε το μέγεθος ομάδας. Μια ομάδα 5 αλόγων μπορεί να αυξηθεί σε μια ομάδα 6, et ainsi de suite και τα λοιπά ανοδική, έτσι ώστε όλες οι πεπερασμένες μεγέθους ομάδες αλόγων πρέπει να είναι το ίδιο χρώμα.
Πράγματι, αφήστε τα δύο άλογα να είναι άλογο Α και άλογο Β. Όταν το άλογο Α απομακρύνεται, είναι αλήθεια ότι τα άλογα παραμονής στο σύνολο είναι το ίδιο χρώμα (μόνο το άλογο Β παραμένει). Εάν το άλογο Β απομακρύνεται αντ' αυτού, αυτό αφήνει ένα διαφορετικό σύνολο μόνο το άλογο Α, το οποίο μπορεί ή δεν να είναι το ίδιο χρώμα με το άλογο Β.
Το πρόβλημα στο επιχείρημα είναι η υπόθεση ότι επειδή καθένα σύνολα περιέχουν μόνο ένα χρώμα των αλόγων, το αρχικό σύνολο περιείχε επίσης μόνο ένα χρώμα των αλόγων. Επειδή δεν υπάρχει κανένα κοινό στοιχείο (άλογα) στα δύο σύνολα, είναι άγνωστο εάν τα δύο άλογα μοιράζονται το ίδιο χρώμα. Κατά συνέπεια το παράδοξο αλόγων δεν είναι αληθινά α παράδοξο, αλλά μόνο το αποτέλεσμα του ραγισμένου συλλογισμού, αν και θα μπορούσε να υποστηριχτεί όλα τα παράδοξα είναι παραδείγματα του ραγισμένου συλλογισμού. Το παράδοξο αλόγων εκθέτει τις παγίδες που προκύπτουν από την αποτυχία να εξεταστούν οι πρόσθετες περιπτώσεις για τις οποίες μια γενική δήλωση μπορεί να είναι ψεύτικη.
4. Το παράδοξο του Γαλιλαίου
( οι φυσικοί είναι όσοι και τα τέλεια τετράγωνα)
Στα μαθηματικά η αντιστοιχία 1-1 των στοιχείων ενός συνόλου με τα στοιχεία ενός άλλου οδηγεί στο συμπέρασμα ότι τα δυο σύνολα έχουν το 'ιδιο πλήθος στοιχείων.
1 -----> 5
2 ------> 7
3 ------> 9
1. ΤΑ ΔΥΟ ΜΠΟΥΚΑΛΙΑ
2. ΕΠΙΣΤΡΟΦΗ ΜΠΟΥΚΑΛΙΩΝ
Στα πλαίσια ενός προγράµµατος ανακύκλωσης, όσοι επιστρέφουν άδεια µπουκάλια κάποιου αναψυκτικού µπορούν να τα ανταλλάξουν µε γεµάτα. Συγκεκριµένα, τα 4 άδεια µπουκάλια ανταλλάσσονται µε 1 γεµάτο. Πόσα µπουκάλια αναψυκτικού θα πιει µια οικογένεια που συγκέντρωσε 24 άδεια µπουκάλια;
3. Η ΛΑΜΠΑ
Έχουµε ένα δωµάτιο το οποίο έχει µία λάµπα(στο εσωτερικό του)και τρεις διακόπτες (στο εξωτερικό του). Ένας από αυτούς τους διακόπτες είναι αυτός που ανάßει την λάµπα. Εµείς πρέπει µε µία µόνο προσπάθεια να καταλάßουµε ποιος διακόπτης είναι ο σωστός.Δηλαδή ποιο ή ποιους διακόπτες πρέπει να πατήσουµε ώστε όταν ανοίξουµε την πόρτα να καταλάßουµε ποιος είναι ο σωστός;
(Εννοείται ότι όταν είναι κλειστή η πόρτα δεν ßλέπουµε αν ανάßει ή όχι η λάµπα).
4. ΤΟ ΠΡΟΒΑΤΟ
Σε ένα κλουßί (σχετικά µεγάλο) είναι κλεισµένα 57 λιοντάρια και 1 πρόßατο. Αν κάποιο λιοντάρι φάει το πρόßατο τότε το πιάνει υπνηλία (από τη ßαρυστοµαχιά) και είναι ευάλωτο σε επιθέσεις άλλου λιονταριού (γίνεται κατά κάποιο τρόπο ψευδό-πρόßατο, δηλαδή υποψήφιο θύµα).
Υποθέστε ότι αν κάποιο λιοντάρι σκοτώσει το θύµα του τότε το τρώει µόνο του (δεν το µοιράζεται µε άλλο λιοντάρι). Επίσης υποθέστε ότι όλα τα λιοντάρια είναι λογικά, και όλα ξέρουν ότι και τα άλλα λιοντάρια σκέφτονται µε λογικό τρόπο. Το κάθε λιοντάρι θέλει κατ' αρχάς να ζήσει και αν µπορεί να φάει κάποιο θύµα τότε θα το κάνει. Οι προτεραιότητές τους δηλαδή είναι (από τη µεγαλύτερη προς τη µικρότερη):
1. Να φάνε το υποψήφιο θύµα και να ζήσουν
5. Ο ΓΕΛΩΤΟΠΟΙΟΣ
Ο ßασιλιάς, που είχε ßαρεθεί το γελωτοποιό του και έψαχνε αφορµή να τον ξεφορτωθεί, τον καλεί µια µέρα και του λέει:
- Πες κάτι, ότι θες. Αν, αυτό που θα πεις, είναι ψέµα θα σε κρεµάσω και αν είναι αλήθεια θα σε σφάξω.
Ο γελωτοποιός στάθηκε για λίγο σκεπτικός και µετά είπε κάτι στον ßασιλιά. Και έζησε!
Τι του είπε;
6. ΟΙ ΠΡΟΤΑΣΕΙΣ
Έχουµε τις παρακάτω δέκα προτάσεις. Ποιες από αυτές είναι αληθείς και ποιες ψευδείς;
1) Μία µόνο από αυτές τις προτάσεις είναι ψευδής.
2) Δύο µόνο από αυτές τις προτάσεις είναι ψευδείς.
3) Τρεις µόνο από αυτές τις προτάσεις είναι ψευδείς.
4) Τέσσερις µόνο από αυτές τις προτάσεις είναι ψευδείς.
5) Πέντε µόνο από αυτές τις προτάσεις είναι ψευδείς.
6) Έξι µόνο από αυτές τις προτάσεις είναι ψευδείς.
7) Επτά µόνο από αυτές τις προτάσεις είναι ψευδείς.
8) Οκτώ µόνο από αυτές τις προτάσεις είναι ψευδείς.
9) Εννέα µόνο από αυτές τις προτάσεις είναι ψευδείς.
10) Δέκα από αυτές τις προτάσεις είναι ψευδείς.
7. ΠΑΝΕΡΙΑ ΜΕ ΦΡΟΥΤΑ
Έχουµε τρία κλειστά πανέρια και µία επιγραφή κρεµασµένη πάνω στο καθένα. Η πρώτη γράφει "ΠΟΡΤΟΚΑΛΙΑ", η δεύτερη γράφει "ΜΑΝΤΑΡΙΝΙΑ" και η τρίτη γράφει "ΠΟΡΤΟΚΑΛΙΑ ΚΑΙ ΜΑΝΤΑΡΙΝΙΑ". Ξέρουµε ότι και οι τρεις επιγραφές είναι τοποθετηµένες λάθος. Πως µπορούµε ßγάζοντας ένα φρούτο από ένα µόνο πανέρι και χωρίς να κοιτάξουµε µέσα ή να ψαχουλέψουµε, να ßάλουµε τις επιγραφές στη σωστή τους θέση;
8. ΟΙ ΜΠΑΛΕΣ
Έχουµε 9 µπάλες του ίδιου όγκου άλλα µία από αυτές έχει διαφορετικό ßάρος, είναι πιο ελαφριά. Ακόµα έχουµε µία ζυγαριά και θέλουµε να ßρούµε την ελαφρύτερη µπάλα κάνοντας µόνο δυο ζυγίσεις.(Η ζυγαριά δεν είναι αυτή που της ßάζεις ένα αντικείµενο και σου λέει το ßάρος του άλλα αυτή που συγκρίνει δυο αντικείµενα για το πιο είναι πιο ßαρύ)
9. ΤΟ ΒΡΑΣΙΜΟ ΤΟΥ ΑΒΓΟΥ
Έχουµε ένα µπρίκι µε νερό που ßράζει και ένα αßγό που πρέπει να ßράσουµε για εννέα λεπτά ακριßώς. Δυστυχώς δεν έχουµε κανένα ρολόι παρά µόνο δύο κλεψύδρες, η µία διάρκειας επτά και η άλλη τεσσάρων λεπτών. Ποιος είναι ο συντοµότερος τρόπος για να µετρήσουµε εννέα λεπτά;
10 ΤΑ ΨΩΝΙΑ
Ένα αντρόγυνο γύριζε από ψώνια στο Σούπερ Μάρκετ φορτωµένοι µε τσάντες. Ο άντρας άρχισε να διαµαρτύρεται στην γυναίκα του ότι οι τσάντες που κουßαλάει είναι πολύ ßαριές. "Τι διαµαρτύρεσαι;" του λέει εκείνη. "Αν µου έδινες µία από τις τσάντες σου, θα είχα τις διπλάσιες απ' ότι εσύ, ενώ αν σου έδινα εγώ µία δικιά µου, θα είχαµε τις ίδιες". Πόσες τσάντες κρατούσε ο καθένας;
11. ΤΡΟΦΗ Ή ΥΠΝΟΣ
Με ποιο τρόπο θα μπορούσαν να έχουν συνεννοηθεί οι κρατούμενοι, αν ήξεραν τους κανόνες του παιχνιδιού, ώστε να μπορέσουν να ζήσουν οι 99 από αυτούς με 100% πιθανότητα και μόνο ένας να ρίσκαρε τη ζωή του με 50% πιθανότητα;
14. ΤΟ ΠΟΤΗΡΙ ΜΕ ΤΟ ΝΕΡΟ
2. Μετακινήστε μόνο 3 σπίρτα και δημιουργήστε 4 τετράγωνα ίδια με το αρχικό μέγεθος

3. Αφαιρέστε δύο σπίρτα ώστε να μείνουν 3. Εύκολο αλλά κρύβει παγίδα!

Β. MAΓΙΚΑ ΤΕΤΡΑΓΩΝΑ
δύο διαγώνιες γραμμές να μας δίνει ως άθροισμα τη Μαγική Σταθερά 165.
Προς διευκόλυνση σας τοποθετήθηκε ήδη στο κέντρο του τετραγώνου ο αριθμός 55.

2. Να συμπληρωθούν τα κενά τετράγωνα του ανωτέρω διαγράμματοςμε τους αριθμούς από το
1-36, ώστε οριζόντια, κάθετα και διαγώνια να μας δίνει τη Μαγική Σταθερά 111.


Ενδιαφέρουσες σπαζοκεφαλιές: εδώ
Γ. sοduko
Για την ιστορία...
Το όνομά του ήρθε στην επικαιρότητα εξαιτίας του δημοφιλούς παιχνιδιού Sudoku, το οποίο και δημιούργησε. Αλλά ο Λέοναρντ Οϊλερ, ο Ελβετός μαθηματικός που έζησε πριν από περίπου 250 χρόνια, ήταν ένας γίγαντας της επιστήμης, μια από τις μεγαλύτερες μορφές των μαθηματικών όλων των εποχών. Αυτή εδώ είναι η ιστορία της πολυτάραχης και, γεμάτης υπολογισμούς..., ζωής του.
* Προσπαθήστε να λύσετε το παρακάτω :

Παίξτε soduko online εδώ κι εδώ αλλά κι εδώ
Δ. ΣΩΣΤΕΣ ΙΣΟΤΗΤΕΣ

Μετακίνησε κατάλληλα μόνο ένα ψηφίο στη κάθε μια ισότητα, ώστε
να γίνουν αληθείς.
 ΑΙΝΙΓΜΑΤΑ
ΑΙΝΙΓΜΑΤΑ
1. Ο ΚΛΕΦΤΗΣ ΚΑΙ ΟΙ ΡΑΒΔΟΙ ΧΡΥΣΟΥ
3. ΟΙ ΠΑΡΤΙΔΕΣ ΣΚΑΚΙ
Πράγματι υπάρχουν πολλές γλώσσες και σήμερα , που αφήνουν τα σύμβολα του γραπτού λόγου να ταιριάζουν , μέσα στο νου μας , στη σωστή έννοια.
α) Αντικείμενα που δεν υπάρχουν
Τα αδύνατα σχήματα είναι η αγαπημένη κατηγορία των ζωγράφων. Τα σχέδια ξεφεύγουν από την πραγματικότητα και μας οδηγούν σε ανύπαρκτους κόσμους. Ο Oscar Rentersvard θεωρείται ο πατέρας των αδύνατων σχημάτων. Έχει δημιουργήσει κατά τη διάρκεια της ζωής του χιλιάδες τέτοια σχήματα , όπως το αδύνατο τρίγωνο , η αδύνατη σκάλα κ.α.
![[LW439.jpg]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgWLH9TJygcr2GWh88rIFMNTplVfgX-Vk31-y2EF20xTGD35yzV3QyQOmNCwcDguPGFhDIPlPIvHlV_3sjr0bKdKQHWw5OtJv0M_rRCx34Qej6lYqymAddw1OFBrIqOumnzI1gL5esTP30/s320/LW439.jpg)
O "Καταρράκτης" του Μάοριτς Κορνέλις Έσερ είναι ένα σκίτσο που δείχνει ένα κανάλι νερού που οδηγείται σε ένα μικρό καταρράκτη. Το νερό πέφτει σε ένα νερόμυλο που βρίσκεται στο επίπεδο από όπου ξεκινά το κανάλι. Όπως καταλαβαίνεις, είναι μια εικόνα αδύνατη, να την κοιτάς και να ζαλίζεσαι, όπως όλες οι εικόνες του Έσερ που έχεις δει κρεμασμένες σε τοίχους φοιτητικών δωματίων.

Η ταινία Μέμπιους είναι μια επιφάνεια που έχει μόνο μία πλευρά αλλά είναι δυνατόν να τη διατρέξει κανείς σε όλο της το μήκος έχοντας την αίσθηση ότι αλλάζει μεριά (κάτι που γίνεται εμφανές και στο σχέδιο του Escher – τα μυρμήγκια βοηθούν σε αυτό). Εύκολα μπορεί κάποιος να φτιάξει αυτό το σχήμα ακόμη και με ένα μακρύ κομμάτι χαρτί του οποίου θα περιστρέψει το ένα άκρο κατά 180 μοίρες και ύστερα θα ενώσει τις άκρες του φτιάχνοντας ένα ενιαίο, συνεχές κομμάτι. Δεν είναι τυχαίο που το σχήμα της ταινίας του Μέμπιους θυμίζει το μαθηματικό σύμβολο του απείρου. Τα μυρμήγκια της εικόνας θα μπορούσαν να προχωρούν για πάντα και να παρέμεναν μονίμως στην ίδια μεριά.
ΕΝΑ ΠΑΝΑΡΧΑΙΟ ΚΙΝΕΖΙΚΟ ΠΑΙΧΝΙΔΙ
ΓΕΩΜΕΤΡΙΚΟΥ ΠΑΖΛ.
( ΔΕΝ ΕΙΝΑΙ ΟΦΘΑΛΜΑΠΑΤΗ )
Το Tangram είναι ένα πολύ παλιό παιχνίδι που επινοήθηκε στην Κίνα γύρω στο 740 π.Χ. Από εκεί εξαπλώθηκε σε όλη την ανατολή και απέκτησε πολλούς φανατικούς φίλους. Λέγεται ότι ακόμα και ο Ναπολέων Βοναπάρτης έπαιζε Tangram με πάθος.
Για να παίξετε, αφού εκτυπώσετε το διπλαν'ο τετράγωνο, κόψτε το περιμετρικά και μετά κατά μήκος της λευκής γραμμής έτσι ώστε να δημιουργηθούν:
• Δύο μεγάλα ορθογώνια και ισοσκελή τρίγωνα.• Ένα μεσαίο ορθογώνιο και ισοσκελές τρίγωνο.
• Δύο μικρά ορθογώνια και ισοσκελή τρίγωνα.
• Ένα τετράγωνο.
• Και ένα πλάγιο παραλληλόγραμμο.
Με αυτά τα 7 γεωμετρικά σχήματα προσπαθήστε να φτιάξετε τα αντικείμενα που βλέπεται παρακάτω. Κανόνας του παιχνιδιού είναι τα κομμάτια να τοποθετούνται το ένα δίπλα στο άλλο ώστε να εφάπτονται οι πλευρές τους και όχι το ένα να καλύπτει μέρος του άλλου.
ΤΟ ΘΕΩΡΗΜΑ ΤΩΝ ΤΕΣΣΑΡΩΝ ΧΡΩΜΑΤΩΝ
Ορισμός του προβλήματος…
Οποιαδόποτε επιφάνεια που χωρίζεται σε περιοχές, όπως ένας πολιτικός χάρτης των νομών ενός κράτους, μπορούν να χρωματιστούν χρησιμοποιώντας λιγότερα από τέσσερα χρώματα κατά τέτοιο τρόπο ώστε καμία από δύο παρακείμενες περιοχές να μην έχουν το ίδιο χρώμα. ήταν το πρώτο σημαντικό θεώρημα που αποδεικνύεται, χρησιμοποιώντας υπολογιστή, και η απόδειξη δεν είναι αποδεκτή από όλους τους μαθηματικούς επειδή θα ήταν αδύνατον για έναν άνθρωπο να το ελέγξει με το χέρι.
Ιστορικά…
Η υπόθεση προτάθηκε αρχικά το 1852, όταν ο φοιτητής Francis Guthrie προσπαθούσε να χρωματίσει το χάρτη των περιφερειών της Αγγλίας.Στα 1976 το θεώρημα των 4 χρωμάτων αποδείχθηκε τελικά από τον Kenneth Appel και Wolfgang Haken από το πανεπιστήμιο του Ιλλινόις . Βοηθήθηκαν από τον John Koch και τον υπολογιστή του (επί 1200 ώρες).

ΤΟ ΘΕΩΡΗΜΑ ΤΗΣ ΠΙΤΣΑΣ.

Αν έχουν στραβοκόψει την πίτσα σας, πώς θα ξέρετε ποιος από τους συνδαιτυμόνες έχει φάει περισσότερο; Ενα τέτοιο πρόβλημα δεν απασχολεί μόνο τους πεινασμένους, αλλά και τους μαθηματικούς που διατύπωσαν- ύστερα από πολλές περιπέτειες- το περίφημο «θεώρημα της πίτσας».
ΤΟΥ STEPHEN ORNES
Η σπαζοκεφαλιά ...
Το πρόβλημα που τους απασχολούσε ήταν το εξής: ας υποθέσουμε ότι στη βιασύνη του ο σερβιτόρος...
κόβει την πίτσα εκτός κέντρου, με όλες τις τομές να διασταυρώνονται σε ένα σημείο σχηματίζοντας ίσες γωνίες με τη γειτονική τους. Οι εκτός κέντρου τομές σημαίνουν ότι τα κομμάτια δεν θα έχουν το ίδιο μέγεθος. Επομένως δύο άτομα που παίρνουν εναλλάξ διαδοχικά κομμάτια, θα έχουν φάει ίσα μερίδια όταν τελειώσει η πίτσα και, αν όχι, ποιος θα έχει φάει περισσότερο;
Οπως συμβαίνει με πολλές μαθηματικές σπαζοκεφαλιές, η απάντηση ήρθε σε στάδια- για διαφορετικές κάθε φορά πιθανές περιπτώσεις του προβλήματος. Η ευκολότερη προσφέρεται όταν τουλάχιστον μία τομή περνάει από το κέντρο της πίτσας: ένα γρήγορο σχήμα μπορεί να δείξει ότι στην περίπτωση αυτή τα αντιδιαμετρικά κομμάτια είναι συμπληρωματικά μεταξύ τους οπότε μοιράζονται ίσα ανάμεσα στους δύο συνδαιτυμόνες, ανεξάρτητα από το πόσες είναι οι τομές.
Διαβάστε περισσότερα εδώ
Διαβάστε περισσότερα εδώ
MAΘΗΜΑΤΙΚΑ ΠΑΡΑΔΟΞΑ
1. Ο Αχιλλέας και η χελώνα ( παράδοξο του Ζήνωνα).
Ο Ζήνωνας, αρχαίος Έλληνας μαθηματικός και φιλόσοφος, είχε θέσει κάποια μαθηματικά παράδοξα που ταλαιπώρησαν τους μαθηματικούς των επόμενων αιώνων στην προσπάθειά τους να δώσουν μια «επιστημονικά σωστή» λύση.
Όπως για παράδειγμα το παράδοξο του Αχιλλέα με τη χελώνα που τρέχουν σ' ένα δρόμο ταχύτητας. Ο Ζήνωνας υποστήριξε ότι, ποτέ ο Αχιλλέας δεν θα καταφέρει να ξεπεράσει την προπορευόμενη χελώνα! Kάθε φορά που o Aχιλλέας θα φτάνει στο σημείο που βρίσκονταν πριν από λίγο η χελώνα, αυτή θα έχει ήδη προχωρήσει (έστω και) λίγο πιο μπροστά… Έτσι αν και ο γοργοπόδαρος Αχιλλέας θα μειώνει συνεχώς την απόσταση απ' την προπορευόμενη χελώνα, ποτέ δεν θα την ξεπεράσει!!!
Παράδοξο που οδηγεί στον απειροστικό λογισμό, όπως και ένα παρόμοιό του, σύμφωνα με το οποίο, ούτε ο Αχιλλέας, αλλά ούτε και η χελώνα θα τερματίσουν ποτέ! Γιατί;
Για να τερματίσουν θα πρέπει πρώτα να φτάσουν στο μέσο της διαδρομής. Όταν φτάσουν στο μέσο θα πρέπει να διανύσουν το πρώτο μισό του εναπομείναντος διαστήματος. Και φυσικά όταν θα το κάνουν αυτό θα πρέπει και πάλι να διανύσουν το επόμενο πρώτο μισό. Και αυτό θα συνεχίζεται επ' άπειρον.
Κι άλλα παράδοξα του Ζήνωνα : εδώ
2. Παράδοξο του κουρέα (παράδοξο του Ράσσελ).
1η διατύπωση
Διατυπώνεται ως εξής: “Σε μια χώρα που όλοι οι άντρες είναι καθημερινά ξυρισμένοι, υπάρχει ένας μόνο κουρέας. Αυτός ξυρίζει όλους τους άντρες που δεν ξυρίζονται μόνοι τους. Τότε όμως ποιος ξυρίζει τον κουρέα;”. Αναλύοντας το πρόβλημα με τη βοήθεια της Θεωρίας των Συνόλων, είναι σαφές ότι στη χώρα υπάρχουν το σύνολο εκείνων που ξυρίζονται μόνοι τους και το σύνολο εκείνων που ξυρίζονται στον κουρέα. Ο κουρέας ξυρίζεται μόνος του;
Αδύνατον, αφού ξυρίζει όλους τους άντρες που δεν ξυρίζονται μόνοι τους. Τον ξυρίζει κάποιος άλλος; Όχι, γιατί ο κουρέας ξυρίζει όλους όσοι δεν ξυρίζονται μόνοι τους. Βρισκόμαστε εδώ μπροστά σ’ ένα παράδοξο. Σύμφωνα με τον Ράσελ, για να το ξεπεράσουμε πρέπει να διορθώσουμε τη δική μας λανθασμένη αντίληψη ότι για κάθε ιδιότητα πρέπει οπωσδήποτε να υπάρχει ένα σύνολο. Σ’ αυτή την περίπτωση δε δημιουργείται κανένα ομοιογενές σύνολο.
2η διατύπωση
Σε ένα χωριό όπου υπάρχει ένας κουρέας οι μισοί άντρες ξυρίζονται στον κουρέα και οι άλλοι μισοί ξυρίζονται μόνοι τους . Ο κουρέας σε ποιά από τις δύο ομάδες ανήκει , σε αυτούς που ξυρίζονται μόνοι τους ή σε αυτούς που τους ξυρίζει ο κουρέας;
3. Το παράδοξο των αλόγων ( όλα τα άλογα έχουν το ίδιο χρώμα)
Υποθέστε ότι έχουμε ένα σύνολο 5 αλόγων. Επιθυμούμε να αποδείξουμε ότι είναι όλο το ίδιο χρώμα. Υποθέστε ότι είχαμε μια απόδειξη ότι όλα τα σύνολα 4 αλόγων ήταν το ίδιο χρώμα. Εάν αυτός ίσχυε, θα μπορούσαμε να αποδείξουμε ότι και τα πέντε άλογα είναι το ίδιο χρώμα με τη διαίρεση των αλόγων σε δύο επικαλύπτοντας ομάδες τεσσάρων αλόγων κάθε ένα. Από την υποτιθέμενη υπάρχουσα απόδειξή μας, δεδομένου ότι αυτές είναι ομάδες 4, όλα τα άλογα σε τα πρέπει να είναι το ίδιο χρώμα. Παραδείγματος χάριν, ο πρώτος, το δευτερόλεπτο, τρίτα και τέταρτα τα άλογα αποτελούν μια ομάδα τεσσάρων, και πρέπει έτσι όλα να είναι το ίδιο χρώμα και τα δεύτερα, τρίτα, τέταρτα και πέμπτα άλογα αποτελούν επίσης μια ομάδα τεσσάρων και πρέπει έτσι επίσης όλα να είναι το ίδιο χρώμα. Για αυτό για να εμφανιστεί, και τα πέντε άλογα στην ομάδα των 5 πρέπει να είναι το ίδιο χρώμα.
Αλλά πώς είμαστε για να πάρουμε μια απόδειξη ότι όλα τα σύνολα 4 αλόγων είναι το ίδιο χρώμα; Εφαρμόζουμε την ίδια λογική πάλι. Με την ίδια διαδικασία, μια ομάδα 4 αλόγων θα μπορούσε να αναλυθεί στις ομάδες 3, και έπειτα μια ομάδα 3 αλόγων θα μπορούσε να αναλυθεί στις ομάδες 2, et ainsi de suite και τα λοιπά. Τελικά θα φθάσουμε σε ένα μέγεθος ομάδας 1, και είναι προφανές ότι όλα τα άλογα σε μια ομάδα 1 αλόγου πρέπει να είναι το ίδιο χρώμα.
Από την ίδια λογική μπορούμε επίσης να αυξήσουμε το μέγεθος ομάδας. Μια ομάδα 5 αλόγων μπορεί να αυξηθεί σε μια ομάδα 6, et ainsi de suite και τα λοιπά ανοδική, έτσι ώστε όλες οι πεπερασμένες μεγέθους ομάδες αλόγων πρέπει να είναι το ίδιο χρώμα.
Εξήγηση
Το επιχείρημα κάνει ανωτέρω την υπονοούμενη υπόθεση ότι τα δύο υποσύνολα από τα άλογα στα οποία η υπόθεση επαγωγής εφαρμόζεται έχει ένα κοινό στοιχείο. Αυτό δεν ισχύει όταν ν = 1, δηλαδή όταν περιέχει μόνο το αρχικό σύνολο 2 άλογα.Πράγματι, αφήστε τα δύο άλογα να είναι άλογο Α και άλογο Β. Όταν το άλογο Α απομακρύνεται, είναι αλήθεια ότι τα άλογα παραμονής στο σύνολο είναι το ίδιο χρώμα (μόνο το άλογο Β παραμένει). Εάν το άλογο Β απομακρύνεται αντ' αυτού, αυτό αφήνει ένα διαφορετικό σύνολο μόνο το άλογο Α, το οποίο μπορεί ή δεν να είναι το ίδιο χρώμα με το άλογο Β.
Το πρόβλημα στο επιχείρημα είναι η υπόθεση ότι επειδή καθένα σύνολα περιέχουν μόνο ένα χρώμα των αλόγων, το αρχικό σύνολο περιείχε επίσης μόνο ένα χρώμα των αλόγων. Επειδή δεν υπάρχει κανένα κοινό στοιχείο (άλογα) στα δύο σύνολα, είναι άγνωστο εάν τα δύο άλογα μοιράζονται το ίδιο χρώμα. Κατά συνέπεια το παράδοξο αλόγων δεν είναι αληθινά α παράδοξο, αλλά μόνο το αποτέλεσμα του ραγισμένου συλλογισμού, αν και θα μπορούσε να υποστηριχτεί όλα τα παράδοξα είναι παραδείγματα του ραγισμένου συλλογισμού. Το παράδοξο αλόγων εκθέτει τις παγίδες που προκύπτουν από την αποτυχία να εξεταστούν οι πρόσθετες περιπτώσεις για τις οποίες μια γενική δήλωση μπορεί να είναι ψεύτικη.
4. Το παράδοξο του Γαλιλαίου
( οι φυσικοί είναι όσοι και τα τέλεια τετράγωνα)
Στα μαθηματικά η αντιστοιχία 1-1 των στοιχείων ενός συνόλου με τα στοιχεία ενός άλλου οδηγεί στο συμπέρασμα ότι τα δυο σύνολα έχουν το 'ιδιο πλήθος στοιχείων.
1 -----> 5
2 ------> 7
3 ------> 9
4 ------> 11
Στο παραπάνω παράδειγμα τα δύο σύνολα των στηλών έχουν ίδιο πλήθος στοιχείων ( πληθάριθμο) γιατί συμβαίνει μία τέτοια αντιστοιχία.
Συμβαίνει το ίδιο όμως όταν τα σύνολα έχουν άπειρο πλήθος στοιχείων;
Ο Γαλιαίος εφάρμοσε αυτό τον κανόνα αντιστοίχισης στους φυσικούς αριθμούς και τα τέλεια τεράγωνο. Τέλειο τετράγωνο λέγεται ο αριθμός που γράφεται ως τετράγωνο ενός φυσικού αριθμού.
π.χ 25 = 5 στο τετράγωνο.
Προσέξτε την παράδοξη αντιστοίχιση :
2
0 ------> 0
2
1 -------> 1
2
2 -----> 2
2
3 -----> 3
2
4 ------> 4
2
5 -------> 5
..................
Σύμφωνα με αυτήν κάθε φυσικός αριθμός αντιστοιχεί στο τετράγωνο του. Άρα όσοι είναι οι φυσικοί τόσα είναι και τα τέλεια τετράγωνα. Πως γίνεται αυτό αφού τα τέλεια τετράγψνα είναι υποσύνολο των φυσικών; Πράγματι τ τέλεια τετράγωνα είναι 0,1,4,9,16,25,36..... Οι φυσικοί είναι περισσότεροι. π.χ ανάμεσα στο 1 και το 4 υπάρχουν ακόμη 3 φυσικοί που δεν είναι τέλεια τετράγωνα.
5. Το παράδοξο του Russell
Σε μια βιβλιοθήκη υπάρχουν κάποιοι κατάλογοι που περιέχουν τίτλους βιβλίων σχετικών με κάποιο θέμα.
Για την καλύτερη εξυπηρέτηση των αναγνωστών, υπάρχουν και κάποιοι πιο γενικοί κατάλογοι οι οποίοι περιέχουν τίτλους των προηγούμενων καταλόγων αναλόγως με το θέμα στο οποίο αναφέρονται.
Από λάθος όμως, μερικοί από αυτούς τους γενικούς καταλόγους περιέχουν και τον τίτλο του εαυτού τους. Όταν ο υπεύθυνος της βιβλιοθήκης αντιλήφθηκε το λάθος αποφάσισε να φτιάξει έναν νέο κατάλογο, τον οποίο ονόμασε «Κατάλογος Σωστών Καταλόγων» και ο οποίος θα περιέχει όλους τους τίτλους των γενικών καταλόγων που δεν περιέχουν τον εαυτό τους.
Και εδώ εμφανίζεται το παράδοξο: Θα πρέπει να συμπεριλάβει στον νέο κατάλογό του τον καινούργιο τίτλο; Αν τον συμπεριλάβει τότε θα περιέχει τον εαυτό του και άρα δεν θα είναι σωστός κατάλογος. Αν δεν τον συμπεριλάβει τότε ο νέος κατάλογος δεν θα περιέχει όλους τους τίτλους των γενικών καταλόγων που δεν περιέχουν τον εαυτό τους.
6. Το παράδοξο του Πρωταγόρα
Στον Πρωταγόρα αποδίδεται το παρακάτω θεωρητικό παράδοξο:
Ο Αρίστιππος ζήτησε από τον Πρωταγόρα να του διδάξει Νομική. Επειδή όμως δεν είχε λεφτά να τον πληρώσει, συμφώνησαν ο Πρωταγόρας να πληρωθεί μόλις ο Αρίστιππος κερδίσει την πρώτη του δίκη.
Ο Αρίστιππος όμως δεν τα κατάφερνε καθόλου καλά στο δικαστήριο και έτσι ο Πρωταγόρας του ζήτησε την καταβολή των χρημάτων του, παρόλο που δεν είχε κερδίσει ακόμα καμία δίκη. Ο Αρίστιππος αρνήθηκε επικαλούμενος τη συμφωνία τους και το θέμα έφτασε στα δικαστήρια.
Ο δικαστής που άκουσε την υπόθεση βρέθηκε στο παρακάτω λογικό παράδοξο:
Αν δικαίωνε τον Αρίστιππο με απόφαση να μην πληρώσει τον Πρωταγόρα τότε ο Αρίστιππος θα είχε μόλις κερδίσει την πρώτη του δίκη και για το λόγο αυτό θα έπρεπε να πληρώσει τον Πρωταγόρα.
Αν από την άλλη, δικαίωνε τον Πρωταγόρα με απόφαση να πληρωθεί από τον Αρίστιππο τότε ο τελευταίος δεν θα είχε κερδίσει ακόμα την πρώτη του δίκη και έτσι δεν θα έπρεπε να πληρώσει τον Πρωταγόρα.
Πως θα βγει ο δικαστής από αυτό το αδιέξοδο;
7. Το διαγώνισμα έκπληξη
Μια Παρασκευή μεσημέρι λέει η δασκάλα στους μαθητές της ότι την επόμενη εβδομάδα θα τους βάλει ένα διαγώνισμα έκπληξη, δηλαδή δεν θα το περιμένουν.
Αφού βγαίνει από την αίθουσα οι μαθητές κάθονται και σκέφτονται ψύχραιμα πως αν το διαγώνισμα δεν έχει μπει μέχρι την ερχόμενη Πέμπτη, τότε η μόνη διαθέσιμη μέρα για να μπει θα είναι η Παρασκευή. Τότε όμως όλοι θα το περιμένουν και άρα δεν θα είναι πια έκπληξη, οπότε η δασκάλα δεν μπορεί να βάλει το διαγώνισμα την Παρασκευή.
Αν περάσει η Τετάρτη και το διαγώνισμα δεν έχει μπει, τότε με δεδομένο ότι δεν μπορεί να μπει ούτε την Παρασκευή, θα πρέπει αναγκαστικά να μπει την Πέμπτη. Και πάλι όμως τότε όλοι θα το περιμένουν, οπότε ούτε και την Πέμπτη μπορεί να μπει το διαγώνισμα.
Συνεχίζοντας αυτή τη συλλογιστική, αποκλείονται μία-μία όλες οι μέρες της εβδομάδας και άρα η δασκάλα δεν μπορεί καμία μέρα να βάλει το διαγώνισμα έκπληξη.
Πως εξηγείται αυτό το παράδοξο;
Πολύ ενδιαφέροντα γεωμετρικά και όχι μόνο παράδοξα καθώς και άλλα διασκεδαστικά μαθηματικά : εδώ
ΒΡΕΣ ΤΟ ΛΑΘΟΣ !
Επίσης εδώ κρύβεται το πανούργο μαθηματικό λάθος. Καταφέρνει να μεταμφιέζεται καταπληκτικά , να καφουφλάρεται πετυχημένα. Μένει απαρατήρητο , ξεγελάει με την λογικοφάνεια του , ξεφεύγει και ξεγλιστράει έντεχνα. Μόνο ένας ξεχωριστός εξερευνητής , ένας δαιμόνιος ντεντέκτιβ σαν εσένα μπορεί να το αποκαλύψει και να το ξεσκεπάσει. Η ανθρωπότητα περιμένει εσένα να το νικήσει. Βάλε όλες τις δυνάμεις και τις δυνατότητές σου , το κοφτερό μυαλό σου και απάλλαξέ μας από την παρουσία του. Κατατρόπωσε τον εχθρό. Ξεσκέπασε το λάθος! Βρες το επιτέλους !
1. Άτοπη ισότητα 1 =2
Πού βρίσκεται το λάθος;
-2 = -2
1 - 3 = 4-6
1-6/2 = 4 - 12/2
1-6/2 + 9/4 = 4 - 12/2 +9/4
12 - ( 2*1*3/2)+(3/2)2 =22 - ( 2 *2*3/2)+(3/2)2
(1-3/2)2 = (2- 3/2)2 τα δυάρια μετά την παρένθεση δηλώνουν εκθέτη.
Χρησιμοποιήσαμε τη ταυτότητα (α +β)2 = α2 +2αβ+β2.
1-3/2 = 2- 3/2
1 =2
2. Άτοπη ισότητα 2 =1
Που είναι το λάθος;
α = β
α2 =αβ
α2-β2 = αβ - β2
(α+β)(α-β) = β(α-β)
α+β = β
2β=β αντικαταστήσαμε το α με β
2 = 1.
3. Ένας ελέφαντας ζυγίζει όσο ένα κουνούπι
Προσπαθήστε να βρείτε που βρίσκεται το λάθος στον παρακάτω υπολογισμό:
1. Έστω πως x είναι το βάρος ενός ελέφαντα και y είναι το βάρος ενός κουνουπιού.
2. Έστω πως 2b είναι το συνολικό τους βάρος. Δηλαδή x + y = 2b
3. Την πιο πάνω εξίσωση μπορούμε να την γράψουμε με δύο τρόπους: Α) x = –y + 2b Β) x – 2b = –y
4. Πολλαπλασιάζουμε κατά μέλη τις εξισώσεις Α και Β και παίρνουμε: x (x – 2b) = –y (–y+2b) <=> x2 – 2xb = y2 – 2yb
5. Προσθέτουμε σε κάθε μέλος της πιο πάνω εξίσωσης το b2 και έχουμε: x2 – 2xb + b2 = y2 – 2yb + b2
6. Παραγοντοποιούμε και τα δύο μέλη με χρήση της γνωστής ταυτότητας: (x – b) 2 = (y – b) 2
7. Παίρνουμε την τετραγωνική ρίζα και των δύο μελών: x – b = y – b
8. Προσθέτουμε το b και στα δύο μέλη: x = y
και καταλήγουμε πως ένας ελέφαντας ζυγίζει όσο ένα κουνούπι!
4 Ανταλλαγή φακέλων
Η Αλίκη και ο Βασίλης τραβάνε στην τύχη από έναν κλειστό φάκελο ο καθένας. Ο οργανωτής του παιχνιδιού τους λέει πως ο κάθε φάκελος έχει μέσα ένα χρηματικό ποσό το οποίο το έχουν ήδη κερδίσει. Τους λέει επίσης ότι ο ένας φάκελος έχει το διπλάσιο ποσό από τον άλλον, χωρίς να τους αποκαλύψει ποιος. Στη συνέχεια τους δίνεται το δικαίωμα αν θέλουν να ανταλλάξουν μεταξύ τους φακέλους.
Η Αλίκη υπολογίζει το κέρδος που αναμένεται να έχει αν δεχτεί να αλλάξει φακέλους ως εξής:
Αν x είναι το ποσό που έχει μέσα ο φάκελός της, τότε με πιθανότητα 1/2 διπλασιάζει το ποσό της, οπότε θα έχει κέρδος x, ενώ με πιθανότητα 1/2 υποδιπλασιάζει το ποσό της, οπότε θα έχει κέρδος -x/2. Σύμφωνα με αυτόν τον συλλογισμό το αναμενόμενο κέρδος της είναι:
(1/2) * x + (1/2) * -x/2 = x/4.
Άρα έχει 25% αναμενόμενο κέρδος αν αλλάξει φακέλους και συνεπώς δέχεται να κάνει την αλλαγή.
Τον ίδιο συλλογισμό κάνει και ο Βασίλης από τη δική του πλευρά και καταλήγει φυσικά στο ίδιο συμπέρασμα, ότι δηλαδή τον συμφέρει κι αυτόν να αλλάξει φακέλους.
Έτσι πραγματοποιείται η αλλαγή. Πριν όμως ανοίξουν τους φακέλους τους και αποκαλυφθούν τα ποσά που κρύβουν, η Αλίκη επαναλαμβάνει τον συλλογισμό της και βρίσκει πως η εκ νέου αλλαγή φακέλων θα της αποφέρει ένα επιπλέον κέρδος λίγο μεγαλύτερο του 25%, το οποίο προκύπτει αν αντί του x στον τύπο βάλουμε το x + x/4 που είναι το ποσό που αναμένει να έχει τώρα στον φάκελό της. Το ίδιο υπολογίζει και ο Βασίλης, οπότε ξανα-αλλάζουν φακέλους και ο καθένας τους θεωρεί πως τώρα έχει ένα αναμενόμενο κέρδος λίγο μεγαλύτερο του 50%. Με το ίδιο σκεπτικό συνεχίζουν να αλλάζουν φακέλους μέχρι να γίνουν και οι δύο πάμπλουτοι.
Στην παραπάνω λογική κάτι πρέπει να πηγαίνει τελείως λάθος, αλλά τι ακριβώς;
5. Απόδειξη πως είμαι ο Πάπας με χρήση Διαφορικού Λογισμού
Την παρακάτω απόδειξη πως είμαι ο Πάπας την έστειλα στο Βατικανό και περιμένω την απάντησή τους για το σχετικό χρίσμα. Λέτε να γίνει δεκτή ή όχι και γιατί;
31 Μαρ

Η ΜΑΓΕΙΑ ΤΩΝ ΑΡΙΘΜΩN

1. Συμμετρία και τελειότητα :
2
1 = 1
2
1 + 2 + 1 = 2
2
1 + 2 + 3 + 2 + 1 = 3
2
1 +2 + 3 +4 + 3 +2 +1 = 4
................................................
2. Ο αριθμός 37 επί τα πολλαπλάσια του 3 :
37 * 3 = 111
37* 6 = 222
37*9 = 333
37 * 12 =444
...................
3. Ο αριθμός 15873 επί τα πολλαπλάσια του 7
15873* 7 = 111111
15873 * 14 = 222222
15873 * 21 = 333333
15873 * 28 = 444444
................................
4. Οι κορυφές των δέντρων
2
9 = 81
2
99 = 9801
2
999 = 998001
2
9999 = 99980001
2
99999 = ;
5 Τα κύματα
12345679 * 9 = 111.111.111
12345678 * 9 = 111.111.102
12345689 *9 = 111.111.201
12345789 *9 = 111.112.101
12346789 *9 = 111.121.101
.........................................
23456789 *9 = 211.111.101
6. Οι μαγικοί αριθμοί
Οι αριθμομνήμονες για να υπολογίσουν γρήγορα γινόμενα μεγάλων αριθμών χρησιμοποιούσαν ως πολλαπλασιαστές κάποιους αριθμούς που τους ονόμαζαν μαγικούς αριθμούς
τέτοιοι είναι : 143 , 1667 , 2.857.143 , 142.857.143.
1.001
143 = -------------
7
5.001
1667 = ------------
3
20.000.001
2.857.143 = ---------------
7
1.000.000.001
142.857.143 = ----------------------
7
1001 862.862
Έτσι όταν ήθελαν να πολλαπλασιάσουν π.χ 143 * 862 = --------- * 862 = ------------= 123.266
7 7
Έκανα δηλαδή τελικά μια εύκολη διαίρεση.
7. Ηπροπαίδεια του 9
Ένας εύκολος τρόπος να θυμάσαι την προπίδεια του 9 είναι ο εξής ;
Γράφεις κατακόρυφα τους αριθμούς από το 0 έως το 9
0
1
2
3
4
5
6
7
8
9
Κατόπιν δίπλα τους ξαναγράφουμε τους ίδιους αριθμούς ξεκινώντας ανάποδα
0 9
1 8
2 7
3 6
4 5
5 4
6 3
7 2
8 1
9 0
Η προπαίδεια του 9 είναι έτοιμη !
8. Η Προπαίδεια του 9 Μέρος 2ο : Με ταχυδακτυλουργία
Άνοιξε τις δύο παλάμες σου. Κλείσε τον αντίχειρα του αριστερού χεριού. Μένουν 9 δάκτυλα ανοικτά.
1* 9 =9
Κλείσε το δεύτερο δάκτυλο του αριστερού χεριού.Αριστερά του κλειστού έχεις 1 ανοικτό και δεξιά 8
2* 9 = 18
Κλείσε το τρίτο δάκτυλο . Αριστερά 2 και δεξιά 7
3*9 = 27
...................................................................
Μέχρι να συνεχίσεις να κλείνεις δάκτυλα και από το δεξί χέρι έχεις όλη την προπαίδεια.
9. Δείτε και τα παρακάτω!
ΜΑΘΗΜΑΤΙΚΟΙ ΓΡΙΦΟΙ
Στο παραπάνω παράδειγμα τα δύο σύνολα των στηλών έχουν ίδιο πλήθος στοιχείων ( πληθάριθμο) γιατί συμβαίνει μία τέτοια αντιστοιχία.
Συμβαίνει το ίδιο όμως όταν τα σύνολα έχουν άπειρο πλήθος στοιχείων;
Ο Γαλιαίος εφάρμοσε αυτό τον κανόνα αντιστοίχισης στους φυσικούς αριθμούς και τα τέλεια τεράγωνο. Τέλειο τετράγωνο λέγεται ο αριθμός που γράφεται ως τετράγωνο ενός φυσικού αριθμού.
π.χ 25 = 5 στο τετράγωνο.
Προσέξτε την παράδοξη αντιστοίχιση :
2
0 ------> 0
2
1 -------> 1
2
2 -----> 2
2
3 -----> 3
2
4 ------> 4
2
5 -------> 5
..................
Σύμφωνα με αυτήν κάθε φυσικός αριθμός αντιστοιχεί στο τετράγωνο του. Άρα όσοι είναι οι φυσικοί τόσα είναι και τα τέλεια τετράγωνα. Πως γίνεται αυτό αφού τα τέλεια τετράγψνα είναι υποσύνολο των φυσικών; Πράγματι τ τέλεια τετράγωνα είναι 0,1,4,9,16,25,36..... Οι φυσικοί είναι περισσότεροι. π.χ ανάμεσα στο 1 και το 4 υπάρχουν ακόμη 3 φυσικοί που δεν είναι τέλεια τετράγωνα.
5. Το παράδοξο του Russell
Σε μια βιβλιοθήκη υπάρχουν κάποιοι κατάλογοι που περιέχουν τίτλους βιβλίων σχετικών με κάποιο θέμα.
Για την καλύτερη εξυπηρέτηση των αναγνωστών, υπάρχουν και κάποιοι πιο γενικοί κατάλογοι οι οποίοι περιέχουν τίτλους των προηγούμενων καταλόγων αναλόγως με το θέμα στο οποίο αναφέρονται.
Από λάθος όμως, μερικοί από αυτούς τους γενικούς καταλόγους περιέχουν και τον τίτλο του εαυτού τους. Όταν ο υπεύθυνος της βιβλιοθήκης αντιλήφθηκε το λάθος αποφάσισε να φτιάξει έναν νέο κατάλογο, τον οποίο ονόμασε «Κατάλογος Σωστών Καταλόγων» και ο οποίος θα περιέχει όλους τους τίτλους των γενικών καταλόγων που δεν περιέχουν τον εαυτό τους.
Και εδώ εμφανίζεται το παράδοξο: Θα πρέπει να συμπεριλάβει στον νέο κατάλογό του τον καινούργιο τίτλο; Αν τον συμπεριλάβει τότε θα περιέχει τον εαυτό του και άρα δεν θα είναι σωστός κατάλογος. Αν δεν τον συμπεριλάβει τότε ο νέος κατάλογος δεν θα περιέχει όλους τους τίτλους των γενικών καταλόγων που δεν περιέχουν τον εαυτό τους.
6. Το παράδοξο του Πρωταγόρα
Στον Πρωταγόρα αποδίδεται το παρακάτω θεωρητικό παράδοξο:
Ο Αρίστιππος ζήτησε από τον Πρωταγόρα να του διδάξει Νομική. Επειδή όμως δεν είχε λεφτά να τον πληρώσει, συμφώνησαν ο Πρωταγόρας να πληρωθεί μόλις ο Αρίστιππος κερδίσει την πρώτη του δίκη.
Ο Αρίστιππος όμως δεν τα κατάφερνε καθόλου καλά στο δικαστήριο και έτσι ο Πρωταγόρας του ζήτησε την καταβολή των χρημάτων του, παρόλο που δεν είχε κερδίσει ακόμα καμία δίκη. Ο Αρίστιππος αρνήθηκε επικαλούμενος τη συμφωνία τους και το θέμα έφτασε στα δικαστήρια.
Ο δικαστής που άκουσε την υπόθεση βρέθηκε στο παρακάτω λογικό παράδοξο:
Αν δικαίωνε τον Αρίστιππο με απόφαση να μην πληρώσει τον Πρωταγόρα τότε ο Αρίστιππος θα είχε μόλις κερδίσει την πρώτη του δίκη και για το λόγο αυτό θα έπρεπε να πληρώσει τον Πρωταγόρα.
Αν από την άλλη, δικαίωνε τον Πρωταγόρα με απόφαση να πληρωθεί από τον Αρίστιππο τότε ο τελευταίος δεν θα είχε κερδίσει ακόμα την πρώτη του δίκη και έτσι δεν θα έπρεπε να πληρώσει τον Πρωταγόρα.
Πως θα βγει ο δικαστής από αυτό το αδιέξοδο;
7. Το διαγώνισμα έκπληξη
Μια Παρασκευή μεσημέρι λέει η δασκάλα στους μαθητές της ότι την επόμενη εβδομάδα θα τους βάλει ένα διαγώνισμα έκπληξη, δηλαδή δεν θα το περιμένουν.
Αφού βγαίνει από την αίθουσα οι μαθητές κάθονται και σκέφτονται ψύχραιμα πως αν το διαγώνισμα δεν έχει μπει μέχρι την ερχόμενη Πέμπτη, τότε η μόνη διαθέσιμη μέρα για να μπει θα είναι η Παρασκευή. Τότε όμως όλοι θα το περιμένουν και άρα δεν θα είναι πια έκπληξη, οπότε η δασκάλα δεν μπορεί να βάλει το διαγώνισμα την Παρασκευή.
Αν περάσει η Τετάρτη και το διαγώνισμα δεν έχει μπει, τότε με δεδομένο ότι δεν μπορεί να μπει ούτε την Παρασκευή, θα πρέπει αναγκαστικά να μπει την Πέμπτη. Και πάλι όμως τότε όλοι θα το περιμένουν, οπότε ούτε και την Πέμπτη μπορεί να μπει το διαγώνισμα.
Συνεχίζοντας αυτή τη συλλογιστική, αποκλείονται μία-μία όλες οι μέρες της εβδομάδας και άρα η δασκάλα δεν μπορεί καμία μέρα να βάλει το διαγώνισμα έκπληξη.
Πως εξηγείται αυτό το παράδοξο;
Πολύ ενδιαφέροντα γεωμετρικά και όχι μόνο παράδοξα καθώς και άλλα διασκεδαστικά μαθηματικά : εδώ
ΒΡΕΣ ΤΟ ΛΑΘΟΣ !
Επίσης εδώ κρύβεται το πανούργο μαθηματικό λάθος. Καταφέρνει να μεταμφιέζεται καταπληκτικά , να καφουφλάρεται πετυχημένα. Μένει απαρατήρητο , ξεγελάει με την λογικοφάνεια του , ξεφεύγει και ξεγλιστράει έντεχνα. Μόνο ένας ξεχωριστός εξερευνητής , ένας δαιμόνιος ντεντέκτιβ σαν εσένα μπορεί να το αποκαλύψει και να το ξεσκεπάσει. Η ανθρωπότητα περιμένει εσένα να το νικήσει. Βάλε όλες τις δυνάμεις και τις δυνατότητές σου , το κοφτερό μυαλό σου και απάλλαξέ μας από την παρουσία του. Κατατρόπωσε τον εχθρό. Ξεσκέπασε το λάθος! Βρες το επιτέλους !
1. Άτοπη ισότητα 1 =2
Πού βρίσκεται το λάθος;
-2 = -2
1 - 3 = 4-6
1-6/2 = 4 - 12/2
1-6/2 + 9/4 = 4 - 12/2 +9/4
12 - ( 2*1*3/2)+(3/2)2 =22 - ( 2 *2*3/2)+(3/2)2
(1-3/2)2 = (2- 3/2)2 τα δυάρια μετά την παρένθεση δηλώνουν εκθέτη.
Χρησιμοποιήσαμε τη ταυτότητα (α +β)2 = α2 +2αβ+β2.
1-3/2 = 2- 3/2
1 =2
2. Άτοπη ισότητα 2 =1
Που είναι το λάθος;
α = β
α2 =αβ
α2-β2 = αβ - β2
(α+β)(α-β) = β(α-β)
α+β = β
2β=β αντικαταστήσαμε το α με β
2 = 1.
3. Ένας ελέφαντας ζυγίζει όσο ένα κουνούπι
Προσπαθήστε να βρείτε που βρίσκεται το λάθος στον παρακάτω υπολογισμό:
1. Έστω πως x είναι το βάρος ενός ελέφαντα και y είναι το βάρος ενός κουνουπιού.
2. Έστω πως 2b είναι το συνολικό τους βάρος. Δηλαδή x + y = 2b
3. Την πιο πάνω εξίσωση μπορούμε να την γράψουμε με δύο τρόπους: Α) x = –y + 2b Β) x – 2b = –y
4. Πολλαπλασιάζουμε κατά μέλη τις εξισώσεις Α και Β και παίρνουμε: x (x – 2b) = –y (–y+2b) <=> x2 – 2xb = y2 – 2yb
5. Προσθέτουμε σε κάθε μέλος της πιο πάνω εξίσωσης το b2 και έχουμε: x2 – 2xb + b2 = y2 – 2yb + b2
6. Παραγοντοποιούμε και τα δύο μέλη με χρήση της γνωστής ταυτότητας: (x – b) 2 = (y – b) 2
7. Παίρνουμε την τετραγωνική ρίζα και των δύο μελών: x – b = y – b
8. Προσθέτουμε το b και στα δύο μέλη: x = y
και καταλήγουμε πως ένας ελέφαντας ζυγίζει όσο ένα κουνούπι!
4 Ανταλλαγή φακέλων
Η Αλίκη και ο Βασίλης τραβάνε στην τύχη από έναν κλειστό φάκελο ο καθένας. Ο οργανωτής του παιχνιδιού τους λέει πως ο κάθε φάκελος έχει μέσα ένα χρηματικό ποσό το οποίο το έχουν ήδη κερδίσει. Τους λέει επίσης ότι ο ένας φάκελος έχει το διπλάσιο ποσό από τον άλλον, χωρίς να τους αποκαλύψει ποιος. Στη συνέχεια τους δίνεται το δικαίωμα αν θέλουν να ανταλλάξουν μεταξύ τους φακέλους.
Η Αλίκη υπολογίζει το κέρδος που αναμένεται να έχει αν δεχτεί να αλλάξει φακέλους ως εξής:
Αν x είναι το ποσό που έχει μέσα ο φάκελός της, τότε με πιθανότητα 1/2 διπλασιάζει το ποσό της, οπότε θα έχει κέρδος x, ενώ με πιθανότητα 1/2 υποδιπλασιάζει το ποσό της, οπότε θα έχει κέρδος -x/2. Σύμφωνα με αυτόν τον συλλογισμό το αναμενόμενο κέρδος της είναι:
(1/2) * x + (1/2) * -x/2 = x/4.
Άρα έχει 25% αναμενόμενο κέρδος αν αλλάξει φακέλους και συνεπώς δέχεται να κάνει την αλλαγή.
Τον ίδιο συλλογισμό κάνει και ο Βασίλης από τη δική του πλευρά και καταλήγει φυσικά στο ίδιο συμπέρασμα, ότι δηλαδή τον συμφέρει κι αυτόν να αλλάξει φακέλους.
Έτσι πραγματοποιείται η αλλαγή. Πριν όμως ανοίξουν τους φακέλους τους και αποκαλυφθούν τα ποσά που κρύβουν, η Αλίκη επαναλαμβάνει τον συλλογισμό της και βρίσκει πως η εκ νέου αλλαγή φακέλων θα της αποφέρει ένα επιπλέον κέρδος λίγο μεγαλύτερο του 25%, το οποίο προκύπτει αν αντί του x στον τύπο βάλουμε το x + x/4 που είναι το ποσό που αναμένει να έχει τώρα στον φάκελό της. Το ίδιο υπολογίζει και ο Βασίλης, οπότε ξανα-αλλάζουν φακέλους και ο καθένας τους θεωρεί πως τώρα έχει ένα αναμενόμενο κέρδος λίγο μεγαλύτερο του 50%. Με το ίδιο σκεπτικό συνεχίζουν να αλλάζουν φακέλους μέχρι να γίνουν και οι δύο πάμπλουτοι.
Στην παραπάνω λογική κάτι πρέπει να πηγαίνει τελείως λάθος, αλλά τι ακριβώς;
5. Απόδειξη πως είμαι ο Πάπας με χρήση Διαφορικού Λογισμού
Την παρακάτω απόδειξη πως είμαι ο Πάπας την έστειλα στο Βατικανό και περιμένω την απάντησή τους για το σχετικό χρίσμα. Λέτε να γίνει δεκτή ή όχι και γιατί;
- Ξεκινάμε με την ισότητα x2 = x * x
- Το δεύτερο μέλος γράφεται x + x + x +…+ x (x φορές)
- Άρα x2 = x + x + x +…+ x (x φορές)
- Παίρνουμε την παράγωγο ως προς x και των δύο μελών: (x2)’ = (x + x + x +…+ x)’
- Επειδή η παράγωγος ενός αθροίσματος ισούται με το άθροισμα των παραγώγων του έχουμε: (x2)’ = x’ + x’ + x’ +…+ x’ (x φορές)
- Υπολογίζουμε τις παραγώγους και στα δύο μέλη: 2x = 1 + 1 + 1 +…+ 1 (x φορές)
- Άρα 2x = x
- Για x <> 0 προκύπτει πως 2 = 1
- Ο Πάπας είναι ένας.
- Κι εγώ είμαι ένας.
- Άρα εγώ και ο Πάπας είμαστε δύο.
- Επειδή όμως στο Βήμα 8 απέδειξα πως 2 = 1, σημαίνει πως εγώ και ο Πάπας είμαστε ένα.
- Άρα εγώ είμαι ο Πάπας!
Πώς αποδεικνύεται ότι π = 4 !
31 Μαρ
20110

Η ΜΑΓΕΙΑ ΤΩΝ ΑΡΙΘΜΩN

1. Συμμετρία και τελειότητα :
2
1 = 1
2
1 + 2 + 1 = 2
2
1 + 2 + 3 + 2 + 1 = 3
2
1 +2 + 3 +4 + 3 +2 +1 = 4
................................................
2. Ο αριθμός 37 επί τα πολλαπλάσια του 3 :
37 * 3 = 111
37* 6 = 222
37*9 = 333
37 * 12 =444
...................
3. Ο αριθμός 15873 επί τα πολλαπλάσια του 7
15873* 7 = 111111
15873 * 14 = 222222
15873 * 21 = 333333
15873 * 28 = 444444
................................
4. Οι κορυφές των δέντρων
2
9 = 81
2
99 = 9801
2
999 = 998001
2
9999 = 99980001
2
99999 = ;
5 Τα κύματα
12345679 * 9 = 111.111.111
12345678 * 9 = 111.111.102
12345689 *9 = 111.111.201
12345789 *9 = 111.112.101
12346789 *9 = 111.121.101
.........................................
23456789 *9 = 211.111.101
6. Οι μαγικοί αριθμοί
Οι αριθμομνήμονες για να υπολογίσουν γρήγορα γινόμενα μεγάλων αριθμών χρησιμοποιούσαν ως πολλαπλασιαστές κάποιους αριθμούς που τους ονόμαζαν μαγικούς αριθμούς
τέτοιοι είναι : 143 , 1667 , 2.857.143 , 142.857.143.
1.001
143 = -------------
7
5.001
1667 = ------------
3
20.000.001
2.857.143 = ---------------
7
1.000.000.001
142.857.143 = ----------------------
7
1001 862.862
Έτσι όταν ήθελαν να πολλαπλασιάσουν π.χ 143 * 862 = --------- * 862 = ------------= 123.266
7 7
Έκανα δηλαδή τελικά μια εύκολη διαίρεση.
7. Ηπροπαίδεια του 9
Ένας εύκολος τρόπος να θυμάσαι την προπίδεια του 9 είναι ο εξής ;
Γράφεις κατακόρυφα τους αριθμούς από το 0 έως το 9
0
1
2
3
4
5
6
7
8
9
Κατόπιν δίπλα τους ξαναγράφουμε τους ίδιους αριθμούς ξεκινώντας ανάποδα
0 9
1 8
2 7
3 6
4 5
5 4
6 3
7 2
8 1
9 0
Η προπαίδεια του 9 είναι έτοιμη !
8. Η Προπαίδεια του 9 Μέρος 2ο : Με ταχυδακτυλουργία
Άνοιξε τις δύο παλάμες σου. Κλείσε τον αντίχειρα του αριστερού χεριού. Μένουν 9 δάκτυλα ανοικτά.
1* 9 =9
Κλείσε το δεύτερο δάκτυλο του αριστερού χεριού.Αριστερά του κλειστού έχεις 1 ανοικτό και δεξιά 8
2* 9 = 18
Κλείσε το τρίτο δάκτυλο . Αριστερά 2 και δεξιά 7
3*9 = 27
...................................................................
Μέχρι να συνεχίσεις να κλείνεις δάκτυλα και από το δεξί χέρι έχεις όλη την προπαίδεια.
9. Δείτε και τα παρακάτω!
The Beauty of Mathematics
1 x 8 + 1 = 9
12 x 8 + 2 = 98
123 x 8 + 3 = 987
1234 x 8 + 4 = 9876
12345 x 8 + 5 = 98765
123456 x 8 + 6 = 987654
1234567 x 8 + 7 = 9876543
12345678 x 8 + 8 = 98765432
123456789 x 8 + 9 = 987654321
9 x 9 + 7 = 88
98 x 9 + 6 = 888
987 x 9 + 5 = 8888
9876 x 9 + 4 = 88888
98765 x 9 + 3 = 888888
987654 x 9 + 2 = 8888888
9876543 x 9 + 1 = 88888888
98765432 x 9 + 0 = 888888888
ΜΑΘΗΜΑΤΙΚΟΙ ΓΡΙΦΟΙ
1. ΤΑ ΔΥΟ ΜΠΟΥΚΑΛΙΑ
Έχετε στη διάθεση σας δύο μπουκάλια. Το πρώτο χωράει 5 λίτρα και το δεύτερο 3. Μπορείτε χρησιμοποιώντας αυτά τα 2 μπουκάλια και απεριόριστη ποσότητα νερού να μετρήσετε ακριβώς 4 λίτρα;
2. ΕΠΙΣΤΡΟΦΗ ΜΠΟΥΚΑΛΙΩΝ
Στα πλαίσια ενός προγράµµατος ανακύκλωσης, όσοι επιστρέφουν άδεια µπουκάλια κάποιου αναψυκτικού µπορούν να τα ανταλλάξουν µε γεµάτα. Συγκεκριµένα, τα 4 άδεια µπουκάλια ανταλλάσσονται µε 1 γεµάτο. Πόσα µπουκάλια αναψυκτικού θα πιει µια οικογένεια που συγκέντρωσε 24 άδεια µπουκάλια;
3. Η ΛΑΜΠΑ
Έχουµε ένα δωµάτιο το οποίο έχει µία λάµπα(στο εσωτερικό του)και τρεις διακόπτες (στο εξωτερικό του). Ένας από αυτούς τους διακόπτες είναι αυτός που ανάßει την λάµπα. Εµείς πρέπει µε µία µόνο προσπάθεια να καταλάßουµε ποιος διακόπτης είναι ο σωστός.Δηλαδή ποιο ή ποιους διακόπτες πρέπει να πατήσουµε ώστε όταν ανοίξουµε την πόρτα να καταλάßουµε ποιος είναι ο σωστός;
(Εννοείται ότι όταν είναι κλειστή η πόρτα δεν ßλέπουµε αν ανάßει ή όχι η λάµπα).
4. ΤΟ ΠΡΟΒΑΤΟ
Σε ένα κλουßί (σχετικά µεγάλο) είναι κλεισµένα 57 λιοντάρια και 1 πρόßατο. Αν κάποιο λιοντάρι φάει το πρόßατο τότε το πιάνει υπνηλία (από τη ßαρυστοµαχιά) και είναι ευάλωτο σε επιθέσεις άλλου λιονταριού (γίνεται κατά κάποιο τρόπο ψευδό-πρόßατο, δηλαδή υποψήφιο θύµα).
Υποθέστε ότι αν κάποιο λιοντάρι σκοτώσει το θύµα του τότε το τρώει µόνο του (δεν το µοιράζεται µε άλλο λιοντάρι). Επίσης υποθέστε ότι όλα τα λιοντάρια είναι λογικά, και όλα ξέρουν ότι και τα άλλα λιοντάρια σκέφτονται µε λογικό τρόπο. Το κάθε λιοντάρι θέλει κατ' αρχάς να ζήσει και αν µπορεί να φάει κάποιο θύµα τότε θα το κάνει. Οι προτεραιότητές τους δηλαδή είναι (από τη µεγαλύτερη προς τη µικρότερη):
1. Να φάνε το υποψήφιο θύµα και να ζήσουν
2. Να µην φάνε το υποψήφιο θύµα και να ζήσουν
3. Να φάνε το υποψήφιο θύµα και να πεθάνουν
Τα λιοντάρια µπορούν να επιζήσουν και χωρίς να φάνε το πρόßατο ή το όποιο άλλο υποψήφιο θύµα (δηλαδή, τους παρέχεται τροφή µε άλλο τρόπο). Η ερώτηση είναι: Θα επιßιώσει το πρόßατο.5. Ο ΓΕΛΩΤΟΠΟΙΟΣ
Ο ßασιλιάς, που είχε ßαρεθεί το γελωτοποιό του και έψαχνε αφορµή να τον ξεφορτωθεί, τον καλεί µια µέρα και του λέει:
- Πες κάτι, ότι θες. Αν, αυτό που θα πεις, είναι ψέµα θα σε κρεµάσω και αν είναι αλήθεια θα σε σφάξω.
Ο γελωτοποιός στάθηκε για λίγο σκεπτικός και µετά είπε κάτι στον ßασιλιά. Και έζησε!
Τι του είπε;
6. ΟΙ ΠΡΟΤΑΣΕΙΣ
Έχουµε τις παρακάτω δέκα προτάσεις. Ποιες από αυτές είναι αληθείς και ποιες ψευδείς;
1) Μία µόνο από αυτές τις προτάσεις είναι ψευδής.
2) Δύο µόνο από αυτές τις προτάσεις είναι ψευδείς.
3) Τρεις µόνο από αυτές τις προτάσεις είναι ψευδείς.
4) Τέσσερις µόνο από αυτές τις προτάσεις είναι ψευδείς.
5) Πέντε µόνο από αυτές τις προτάσεις είναι ψευδείς.
6) Έξι µόνο από αυτές τις προτάσεις είναι ψευδείς.
7) Επτά µόνο από αυτές τις προτάσεις είναι ψευδείς.
8) Οκτώ µόνο από αυτές τις προτάσεις είναι ψευδείς.
9) Εννέα µόνο από αυτές τις προτάσεις είναι ψευδείς.
10) Δέκα από αυτές τις προτάσεις είναι ψευδείς.
7. ΠΑΝΕΡΙΑ ΜΕ ΦΡΟΥΤΑ
Έχουµε τρία κλειστά πανέρια και µία επιγραφή κρεµασµένη πάνω στο καθένα. Η πρώτη γράφει "ΠΟΡΤΟΚΑΛΙΑ", η δεύτερη γράφει "ΜΑΝΤΑΡΙΝΙΑ" και η τρίτη γράφει "ΠΟΡΤΟΚΑΛΙΑ ΚΑΙ ΜΑΝΤΑΡΙΝΙΑ". Ξέρουµε ότι και οι τρεις επιγραφές είναι τοποθετηµένες λάθος. Πως µπορούµε ßγάζοντας ένα φρούτο από ένα µόνο πανέρι και χωρίς να κοιτάξουµε µέσα ή να ψαχουλέψουµε, να ßάλουµε τις επιγραφές στη σωστή τους θέση;
8. ΟΙ ΜΠΑΛΕΣ
Έχουµε 9 µπάλες του ίδιου όγκου άλλα µία από αυτές έχει διαφορετικό ßάρος, είναι πιο ελαφριά. Ακόµα έχουµε µία ζυγαριά και θέλουµε να ßρούµε την ελαφρύτερη µπάλα κάνοντας µόνο δυο ζυγίσεις.(Η ζυγαριά δεν είναι αυτή που της ßάζεις ένα αντικείµενο και σου λέει το ßάρος του άλλα αυτή που συγκρίνει δυο αντικείµενα για το πιο είναι πιο ßαρύ)
9. ΤΟ ΒΡΑΣΙΜΟ ΤΟΥ ΑΒΓΟΥ
Έχουµε ένα µπρίκι µε νερό που ßράζει και ένα αßγό που πρέπει να ßράσουµε για εννέα λεπτά ακριßώς. Δυστυχώς δεν έχουµε κανένα ρολόι παρά µόνο δύο κλεψύδρες, η µία διάρκειας επτά και η άλλη τεσσάρων λεπτών. Ποιος είναι ο συντοµότερος τρόπος για να µετρήσουµε εννέα λεπτά;
10 ΤΑ ΨΩΝΙΑ
Ένα αντρόγυνο γύριζε από ψώνια στο Σούπερ Μάρκετ φορτωµένοι µε τσάντες. Ο άντρας άρχισε να διαµαρτύρεται στην γυναίκα του ότι οι τσάντες που κουßαλάει είναι πολύ ßαριές. "Τι διαµαρτύρεσαι;" του λέει εκείνη. "Αν µου έδινες µία από τις τσάντες σου, θα είχα τις διπλάσιες απ' ότι εσύ, ενώ αν σου έδινα εγώ µία δικιά µου, θα είχαµε τις ίδιες". Πόσες τσάντες κρατούσε ο καθένας;
11. ΤΡΟΦΗ Ή ΥΠΝΟΣ
Ας υποθέσουμε ότι ένας άνθρωπος μπορεί να επιβιώσει δύο εβδομάδες χωρίς τροφή και χωρίς ύπνο. Τι θα έπρεπε να κάνει κάποιος μετά από δεκατέσσερις ημέρες χωρίς φαγητό και χωρίς ύπνο; Να φάει ή να κοιμηθεί πρώτα;
12. ΟΛΑ ΓΙΑ ΕΝΑ ΠΑΓΩΤΟ
Δυο αδέλφια, ο Μπόρις και η Μαρίνα θέλουν να αγοράσουν παγωτά, έχουν όμως κάποιο πρόβλημα. Ο Μπόρις έχει 24 καπίκια λιγότερα από όσα του χρειάζονται για να αγοράσει ένα παγωτό και η Μαρίνα έχει 2 καπίκια λιγότερα από την αξία του παγωτού. Αποφασίζουν λοιπόν, μιας και δε μπορούν να αγοράσουν δύο παγωτά, να αγοράσουν μόνο ένα, ενώνοντας τα χρήματα τους. Και πάλι όμως τα χρήματα τους δεν είναι αρκετά για να αγοράσουν έστω το ένα παγωτό. Πόσο κοστίζει το παγωτό;
13. ΟΙ ΚΡΑΤΟΥΜΕΝΟΙ
Είναι 100 κρατούμενοι σε μία φυλακή και μία μέρα έρχεται ένας φρουρός και τους λέει: «Σήμερα το βράδυ θα παίξουμε ένα… παιχνίδι». Το βράδυ λοιπόν όταν έρχεται, κλείνει τα μάτια σε όλους και φοράει ένα καπέλο στον καθένα. Τα καπέλα έχουν είτε άσπρο είτε μαύρο χρώμα. Αμέσως μετά τους τοποθετεί, ανακατεμένους τυχαία, σε μία ευθεία γραμμή στοιχισμένους στη σειρά με τρόπο τέτοιο ώστε ο καθένας να κοιτάει μόνο μπροστά του και ποτέ πίσω. Δηλαδή, καθένας να μπορεί να δει όλους τους μπροστινούς του αλλά κανέναν πίσω του. Ακολούθως σε σε μία επίδειξη δύναμης και αλαζονείας τους λέει ότι θα ξεκινήσει να τους ρωτάει από το τέλος προς την αρχή (δηλαδή από εκείνον που κοιτάει όλους τους άλλους και δεν έχει κανέναν πίσω του) τι χρώμα καπέλο φοράει ο καθένας. Όποιος απαντά λάθος θα εκτελείται, όποιος απαντά σωστά θα του χαρίζεται η ζωή.
Η ερώτηση είναι η εξής:Με ποιο τρόπο θα μπορούσαν να έχουν συνεννοηθεί οι κρατούμενοι, αν ήξεραν τους κανόνες του παιχνιδιού, ώστε να μπορέσουν να ζήσουν οι 99 από αυτούς με 100% πιθανότητα και μόνο ένας να ρίσκαρε τη ζωή του με 50% πιθανότητα;
14. ΤΟ ΠΟΤΗΡΙ ΜΕ ΤΟ ΝΕΡΟ
Είστε σε ένα κενό δωμάτιο και έχετε ένα διαφανές ποτήρι με νερό. Το ποτήρι είναι ένας τέλειος κύλινδρος, και μοιάζει να είναι κατά το ήμισυ γεμάτο, αλλά δεν είστε βέβαιος. Πώς μπορείτε να υπολογίσετε εάν το ποτήρι είναι κατά το ήμισυ γεμάτο, περισσότερο από το μισό, ή λιγότερο από το μισό; Δεν έχετε στην διάθεση σας κανένα εργαλείο ή χάρακα κτλ.
15. ΟΙ ΚΑΜΗΛΕΣ ΚΑΙ Ο ΣΟΦΟΣ
Ένα άραβας σεΐχης, μεγάλος σε ηλικία, θέλει να αφήσει την περιουσία του σε ένα από τα δύο του παιδιά. Αποφασίζει λοιπόν το εξής: οι δυο του γιοι θα τρέξουν τις καμήλες τους σε ένα αγώνα και όποια καμήλα τερματίσει τελευταία ο ιδιοκτήτης θα κερδίσει την περιουσία. Κατά τη διάρκεια του αγώνα, οι δύο αδελφοί περιπλανιούνται για μέρες, χωρίς κανένας να είναι πρόθυμος να διασχίσει τη γραμμή του τέρματος. Μέσα στην απογοήτευση τους, ρωτούν ένα σοφό άτομο για την συμβουλή του. Τους λέει κάτι και έπειτα οι δύο αδελφοί ανεβαίνουν σφαίρα πάνω στις καμήλες και κατευθύνονται με ταχύτητα προς τη γραμμή τέρματος. Τι τους είπε ο σοφός;
16 Ο ΒΑΤΡΑΧΟΣ ΚΑΙ ΤΟ ΠΗΓΑΔΙ.
Ένας βάτραχος από την περιέργεια του έπεσε μέσα σε ένα πηγάδι 10 μέτρα. Κάθε μέρα ο βάτραχος προσπαθεί να βγεί και ανεβαίνει 3 μέτρα. Το βράδυ όμως γλιστράει κατά 2 μέτρα πίσω στο πηγάδι. Σε πόσες μέρες θα καταφέρει να βγεί έξω;
ΣΠΑΖΟΚΕΦΑΛΙΕΣ
Α. ... ΜΕ ΣΠΙΡΤΑ!
1. Έχουμε λοιπόν τα 16 σπίρτα τοποθετημένα όπως τα βλέπετε στο σχήμα της εικόνας. Το ζητούμενο είναι, αν είναι βέβαια εφικτό, αλλάζοντας θέση σε 2 μόνο σπίρτα και χρησιμοποιώντας πάλι και τα 16 σπίρτα (δεν μπορείτε απλά να εξαφανίσετε δύο σπίρτα) να σχηματιστούν 4 τετράγωνα που να μην έχουν καμία πλευρά κοινή. Το Εγχοιρίδιο εύχεται καλή επιτυχία σε όλους!
ΣΠΑΖΟΚΕΦΑΛΙΕΣ
Α. ... ΜΕ ΣΠΙΡΤΑ!
1. Έχουμε λοιπόν τα 16 σπίρτα τοποθετημένα όπως τα βλέπετε στο σχήμα της εικόνας. Το ζητούμενο είναι, αν είναι βέβαια εφικτό, αλλάζοντας θέση σε 2 μόνο σπίρτα και χρησιμοποιώντας πάλι και τα 16 σπίρτα (δεν μπορείτε απλά να εξαφανίσετε δύο σπίρτα) να σχηματιστούν 4 τετράγωνα που να μην έχουν καμία πλευρά κοινή. Το Εγχοιρίδιο εύχεται καλή επιτυχία σε όλους!
2. Μετακινήστε μόνο 3 σπίρτα και δημιουργήστε 4 τετράγωνα ίδια με το αρχικό μέγεθος

3. Αφαιρέστε δύο σπίρτα ώστε να μείνουν 3. Εύκολο αλλά κρύβει παγίδα!

Β. MAΓΙΚΑ ΤΕΤΡΑΓΩΝΑ
1. Στο παρακάτω Μαγικό Τετράγωνο (3x3), της τρίτης τάξεως, να τοποθετηθούν
οι κάτωθι παλίνδρομοι αριθμοί: 11, 22, 33, 44, 66, 77, 88, 99
με τέτοιο τρόπο ώστε σε κάθε οριζόντια γραμμή, σε κάθε κάθετη γραμμή, και στιςοι κάτωθι παλίνδρομοι αριθμοί: 11, 22, 33, 44, 66, 77, 88, 99
δύο διαγώνιες γραμμές να μας δίνει ως άθροισμα τη Μαγική Σταθερά 165.
Προς διευκόλυνση σας τοποθετήθηκε ήδη στο κέντρο του τετραγώνου ο αριθμός 55.

2. Να συμπληρωθούν τα κενά τετράγωνα του ανωτέρω διαγράμματοςμε τους αριθμούς από το
1-36, ώστε οριζόντια, κάθετα και διαγώνια να μας δίνει τη Μαγική Σταθερά 111.
Προς διευκόλυνση σας ήδη έχουν τοποθετηθεί ορισμένοι από τους ζητούμενους αριθμούς.


Γ. sοduko
Για την ιστορία...
Το όνομά του ήρθε στην επικαιρότητα εξαιτίας του δημοφιλούς παιχνιδιού Sudoku, το οποίο και δημιούργησε. Αλλά ο Λέοναρντ Οϊλερ, ο Ελβετός μαθηματικός που έζησε πριν από περίπου 250 χρόνια, ήταν ένας γίγαντας της επιστήμης, μια από τις μεγαλύτερες μορφές των μαθηματικών όλων των εποχών. Αυτή εδώ είναι η ιστορία της πολυτάραχης και, γεμάτης υπολογισμούς..., ζωής του.
* Προσπαθήστε να λύσετε το παρακάτω :

Παίξτε soduko online εδώ κι εδώ αλλά κι εδώ
Δ. ΣΩΣΤΕΣ ΙΣΟΤΗΤΕΣ
1. Στην παρακάτω ισότητα προσθέστε, σε οποιοδήποτε σύμβολο της
πρόσθεσης, μια γραμμή, έτσι ώστε να είναι σωστή.
2. Δίδονται οι παρακάτω ψευδείς ισότητες:
να γίνουν αληθείς.
1. Ο ΚΛΕΦΤΗΣ ΚΑΙ ΟΙ ΡΑΒΔΟΙ ΧΡΥΣΟΥ
Ένας κλέφτης κατόρθωσε να κλέψει δύο ράβδους χρυσού από τον βασιλιά. Καθώς τον κυνηγούσαν οι φρουροί, βρέθηκε μπροστά σε μία γέφυρα, με μία πινακίδα που έγραφε ότι το μέγιστο βάρος που μπορούσε να αντέξει ήταν 80 κιλά. Δυστυχώς ο ίδιος ζύγιζε 76 κιλά και η κάθε μία από τις ράβδους 3 κιλά. Μήπως είχε έρθει η ώρα να αποχωριστεί τη μία ράβδο;
(Απάντηση: Ο κλέφτης μπόρεσε να περάσει και τις δύο ράβδους ταυτόχρονα απέναντι, κάνοντας ένα ζογκλερικό κόλπο: Πέταξε τη μία ψηλά και άρχισε να διασχίζει τη γέφυρα. Λίγο πριν την ξαναπιάσει, πέταξε ψηλά την άλλη, κ.ο.κ., μέχρι που πέρασε και με τις δύο.)
(Απάντηση: Ο κλέφτης μπόρεσε να περάσει και τις δύο ράβδους ταυτόχρονα απέναντι, κάνοντας ένα ζογκλερικό κόλπο: Πέταξε τη μία ψηλά και άρχισε να διασχίζει τη γέφυρα. Λίγο πριν την ξαναπιάσει, πέταξε ψηλά την άλλη, κ.ο.κ., μέχρι που πέρασε και με τις δύο.)
2. ΕΣΥ ΚΑΙ Η ΜΗΤΕΡΑ ΣΟΥ
Πως είναι δυνατόν να σταθείς πίσω ακριβώς από την μητέρα σου κι εκείνη ακριβώς πίσω από σένα ;
( Απάντηση : θα σταθείτε πλάτη με πλάτη ).
Ο Χρήστος κι ο Λάμπρος έπαιζαν σκάκι. Έπαιξαν συνολικά 7 παρτίδες. Κάθε ένας απ αυτούς έκανε τον ίδιο αριθμό νικών και καμία παρτίδα από όσες έπαιξαν δεν έληξε ισόπαλη. Είναι αυτό δυνατό ;
Απάντηση : Ναι, αν δεν έπαιζαν μεταξύ τους.
4. ΤΑ ΔΙΔΥΜΑ
 Είναι γνωστό πως ότι ημέρα πέσουν τα Χριστούγεννα την ίδια μέρα πέφτει και η Πρωτοχρονιά. Κι όμως το 1939 τα Χριστούγεννα έπεσαν Δευτέρα και η Πρωτοχρονιά Κυριακή. Πως έγινε αυτό ;
Είναι γνωστό πως ότι ημέρα πέσουν τα Χριστούγεννα την ίδια μέρα πέφτει και η Πρωτοχρονιά. Κι όμως το 1939 τα Χριστούγεννα έπεσαν Δευτέρα και η Πρωτοχρονιά Κυριακή. Πως έγινε αυτό ;
4. ΤΑ ΔΙΔΥΜΑ
<< Κάθε χρονιά τα Χριστούγεννα και η Πρωτοχρονιά πέφτουν διαφορετικές ημέρες. Είναι τα Χριστούγεννα και η Πρωτοχρονιά της επόμενης χρονιάς που πέφτουν πάντα την ίδια μέρα. >>
5. ΤΟ ΑΝΟΙΓΜΑ ΤΗΣ ΓΩΝΙΑΣ
Αν κοιτάξουμε μια γωνία με ένα μεγεθυντικό φακό που μεγεθύνει τα πάντα κατά 3 φορές και την βρούμε να είναι 45 μοίρες πόσες μοίρες θα είναι αν την δούμε χωρίς τον φακό ;
<< Ποτέ. Σε κάθε «μονό» κύκλο ο μπαμπάς θα βγάζει το δεξί και το παιδί το αριστερό. Σε κάθε «ζυγό» κύκλο θα βγάζουν και οι δύο το δεξί. >>
7. ΤΑ ΑΤΑΚΤΑ ΑΔΕΡΦΙΑ ΚΑΙ Η ΕΦΗΜΕΡΙΔΑ
Ο Τάκης κι ο Μάκης, δύο άτακτα αγόρια τσακώνονταν για μια σελίδα από την εφημερίδα. Η μητέρα τους για να τους τιμωρήσει τους έβαλε να στέκονται όρθιοι πατώντας πάνω στην εφημερίδα στραμμένοι ο ένας απέναντι στον άλλον. Παρ’ όλο που η σελίδα της εφημερίδας δεν σκίστηκε ο Τάκης δεν μπορούσε να δει τον αδελφό του. Πως γίνεται ;
8. ΤΑ ΧΑΠΙΑ
Αν ο γιατρός σας σας δώσει 3 χάπια και σας πει να τα πάρετε με μισή ώρα διαφορά το ένα από το άλλο, πόση ώρα θα περάσει μέχρι να τα πάρετε και τα τρία ;
Αν κοιτάξουμε μια γωνία με ένα μεγεθυντικό φακό που μεγεθύνει τα πάντα κατά 3 φορές και την βρούμε να είναι 45 μοίρες πόσες μοίρες θα είναι αν την δούμε χωρίς τον φακό ;
Απάντηση : Το άνοιγμα μιας γωνίας δεν επηρεάζεται από καμία μεγέθυνση. ( Θεωρία ομοίων τριγώνων).
6. ΤΟ ΒΑΔΙΣΜΑ ΠΑΤΕΡΑ - ΓΙΟΥ
Ένας μπαμπάς ξεκινάει με το παιδί του μια βόλτα. Ξεκινούν και οι δύο με το δεξί πόδι πρώτο. Ο μπαμπάς κάνει δύο βήματα σε κάθε «κύκλο» βαδίσματος ενώ το παιδάκι του τρία. Πότε θα βγάλουν και οι δύο το αριστερό τους πόδι ταυτόχρονα μπροστά ;
<< Ποτέ. Σε κάθε «μονό» κύκλο ο μπαμπάς θα βγάζει το δεξί και το παιδί το αριστερό. Σε κάθε «ζυγό» κύκλο θα βγάζουν και οι δύο το δεξί. >>
7. ΤΑ ΑΤΑΚΤΑ ΑΔΕΡΦΙΑ ΚΑΙ Η ΕΦΗΜΕΡΙΔΑ
Ο Τάκης κι ο Μάκης, δύο άτακτα αγόρια τσακώνονταν για μια σελίδα από την εφημερίδα. Η μητέρα τους για να τους τιμωρήσει τους έβαλε να στέκονται όρθιοι πατώντας πάνω στην εφημερίδα στραμμένοι ο ένας απέναντι στον άλλον. Παρ’ όλο που η σελίδα της εφημερίδας δεν σκίστηκε ο Τάκης δεν μπορούσε να δει τον αδελφό του. Πως γίνεται ;
<< Η μητέρα είχε βάλει την εφημερίδα κάτω από την χαραμάδα μιας πόρτας. Και τα δύο αγόρια πατούσαν πάνω της απέναντι το ένα στο άλλο αλλά με την πόρτα κλειστή δεν μπορούσαν να δουν ο ένας τον άλλον. >>
8. ΤΑ ΧΑΠΙΑ
Αν ο γιατρός σας σας δώσει 3 χάπια και σας πει να τα πάρετε με μισή ώρα διαφορά το ένα από το άλλο, πόση ώρα θα περάσει μέχρι να τα πάρετε και τα τρία ;
<< Μία ώρα. Μισή μεταξύ πρώτο και δεύτερου και άλλη μισή μεταξύ δεύτερου και τρίτου >>
9. ΟΙ ΚΑΛΤΣΕΣ
Σε ένα συρτάρι έχετε 12 ζευγάρια άσπρες και 12 ζευγάρια μαύρες κάλτσες. Χωρίς να βλέπετε, πόσες κάλτσες πρέπει να τραβήξετε για να είστε σίγουροι πως έχετε στα χέρια σας τουλάχιστον ένα ζευγάρι όμοιες κάλτσες ?
<< 3 κάλτσες. >>
10. ΟΙ ΤΑΞΙΔΙΩΤΕΣ
Τρεις ταξιδιώτες φτάνουν σε ένα ξενοδοχείο. Ο υπάλληλος τους ενημερώνει ότι πρέπει να πληρώσει καθένας τους από 10.000 δραχμές, άρα σύνολο 30.000 δραχμές και οι τρεις μαζί. Αργότερα όμως ο υπάλληλος του ξενοδοχείου συνειδητοποιεί ότι έκανε λάθος και έπρεπε να χρεώσει μόνον 25.000 δραχμές αντί για 30.000. Δίνει λοιπόν 5.000 δραχμές στον αχθοφόρο για να τις επιστρέψει στους ταξιδιώτες. Ο πονηρός αχθοφόρος επιστρέφει μόνον 1.000 δραχμές σε καθέναν από τους ταξιδιώτες και κρατά για τον εαυτό του τις υπόλοιπες 2.000 δραχμές. Άρα οι τρεις ταξιδιώτες ξόδεψαν 27.000 δραχμές και ο αχθοφόρος κράτησε 2.000 δραχμές. Τι απέγιναν οι 1.000 δραχμές μέχρι τις 30.000 που αρχικά ξόδεψαν οι τρεις ταξιδιώτες ?
<< Δεν λείπουν 1.000 δραχμές. Οι τρεις ταξιδιώτες ξόδεψαν 25.000 για το ξενοδοχείο και 2.000 για τον αχθοφόρο…! >>









Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου