" Παρουσιάζουμε τα μαθηματικά σαν κανείς να μη τα δημιούργησε , σαν να μη γεννήθηκαν για να εξυπηρετήσουν συγκεκριμένες ανάγκες , σα να στεκόταν πάντα εκεί ακίνητα και στατικά όπως τα βουνά και τα ποτάμια "
Αεί ο Θεός ο μέγας γεωμετρεί
το κύκλου μήκος ίνα ορίση διαμέτρω
παρήγαγεν αριθμόν απέραντον
και ον φευ! ουδέποτε όλον θνητοί θα εύρωσι.
Αν γράφουμε τους αριθμούς των γραμμάτων που περιέχει κάθε λέξη του πίήματος έχουμε τα πρώτα 22 δεκαδικά ψηφία του π.
Βέβαια θα μπορούσε κανείς να αντιτάξει ότι «τέτοιου είδους αριθμός δεν κυκλοφορεί στις γειτονιές της Πραγματικότητας». Όμως υπάρχει αλήθεια αριθμός που να έχει πραγματική υπόσταση; βλέπουμε κανένα 2; πιάνουμε κανένα 14; ακούμε κανένα -5; επομένως όλοι οι αριθμοί είναι κατ’ ουσίαν «φανταστικοί».
Εξάλλου μία ανάλογη απάντηση σε διαφορετικό βέβαια ερώτημα είχε δοθεί από τους Ινδούς μαθηματικούς πριν από αρκετούς αιώνες. Ήταν τότε που η ανάγκη για μία απάντηση στο ερώτημα «με τι ισούται η διαφορά 1-2 ; » είχε οδηγήσει στην επινόηση των αρνητικών αριθμών .
Στη συγκεκριμένη περίπτωση της τετραγωνικής ρίζας του «-1 » μία σημασιακή διεύρυνση της έννοιας αριθμός θα μπορούσε να είναι τέτοια ώστε να χωρέσει και το καινούριο πλάσμα της ανθρώπινης αφαιρετικής σκέψης. Και αυτό συνέβη. Ο Bombelli «έσπρωξε» στο παλκοσένικο της ιστορίας των Μαθηματικών αριθμούς όπως ο R[Om. 9] -στον οποίο το R παριστάνει την τετραγωνική ρίζα και το m το πρόσημο «μείον» και τον οποίο θα συμβολίζαμε σήμερα με Ö(0-9) – .
Ο αλλόκοτος αυτός αριθμός, γέννημα θρέμμα της Ευρώπης, που χαρακτηρίστηκε από τον Descartes «imaginaire» – στην ελληνική γλώσσα «φανταστικός»- έκανε την εμφάνισή του χωρίς να συμβολίζεται με κάποιο γενικώς αποδεκτό σύμβολο. Ο φανταστικός αριθμός γεννήθηκε λοιπόν τον 16ο αιώνα και απέκτησε τον δικό του «παγκόσμιο» συμβολισμό με το γράμμα i τον 18ο αιώνα ύστερα από πρόταση του Euler.
Επόμενο ήταν η δημιουργία ενός νέου συνόλου αριθμών -υποσύνολοτου οποίου είναι το R-, το C, δηλαδή αυτό των μιγαδικών. Οι αριθμοί αυτοί έχουν τη μορφή χ + yi, με τους χ και y να ανήκουν στο R. Οι γνωστοί σε όλους μας λοιπόν πραγματικοί αριθμοί προκύπτουν μηδενίζοντας το φανταστικό μέρος των μιγαδικών, δηλαδή το y, παίρνοντας τη μορφή χ + 0*i = x. Aνίστοιχα οι φανταστικοί προκύπτουν με μηδενισμό του πραγματικού μέρους των μιγαδικών. Αναδιατυπώνουμε λοιπόν, με μαθηματική χροιά, όλοι οι αριθμοί είναι μιγαδικοί!
Το πρόβλημα βέβαια που δημιουργήθηκε είναι ότι όλοι αυτοί οι φανταστικοί και οι μιγαδικοί αριθμοί δεν έχουν θέση στην ευθεία των πραγματικών αριθμών. Οι μαθηματικοί όμως ξεπέρασαν και αυτή τη δυσκολία δημιουργώντας, την ευθεία των φανταστικών αριθμών κάθετη στην ευθεία των πραγματικών αριθμών και από τότε, ενώ οι πραγματικοί εξακολουθούν να κυκλοφορούν στη δική τους ευθεία, οι φανταστικοί «ζουν» πάνω στην άλλη. Όσο για τους μιγαδικούς, αυτοί ζουν στο επίπεδο των δύο αυτών ευθειών.
Οι μιγαδικοί αριθμοί έχουν, μεταξύ άλλων, σημαντικές εφαρμογές στη λύση διαφορικών εξισώσεων αλλά και στη μελέτη διάφορων φυσικών προβλημάτων οπτικής, κυματικής, κβαντομηχανικής και ηλεκτρονικής
7. Ιστορία των εξισώσεων : εδώ
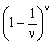όταν το ν είναι πάρα πολύ μεγάλο, ως βάση για λογαρίθμους.
12. ΘΑΛΗΣ ο ΜΙΛΗΣΙΟΣ
δ΄.[4]
Ἐὰν δύο τρίγωνα τὰς δύο πλευρὰς [ταῖς] δυσὶ πλευραῖς ἴσας ἔχῃ ἑκατέραν ἑκατέρᾳ καὶ τὴν γωνίαν τῇ γωνίᾳ ἴσην ἔχῃ τὴν ὑπὸ τῶν ἴσων εὐθειῶν περιεχομένην, καὶ τὴν βάσιν τῇ βάσει ἴσην ἕξει, καὶ τὸ τρίγωνον τῷ τριγώνῳ ἴσον ἔσται, καὶ αἱ λοιπαὶ γωνίαι ταῖς λοιπαῖς γωνίαις ἴσαι ἔσονται ἑκατέρα ἑκατέρᾳ, ὑφ' ἃς αἱ ἴσαι πλευραὶ ὑποτείνουσιν.
ε΄.[5]
Τῶν ἰσοσκελῶν τριγώνων αἱ πρὸς τῇ βάσει γωνίαι ἴσαι ἀλλήλαις εἰσίν, καὶ προσεκβληθεισῶν τῶν ἴσων εὐθειῶν αἱ ὑπὸ τὴν βάσιν γωνίαι ἴσαι ἀλλήλαις ἔσονται.
Εκτεταμένα αποσπάσματα των Στοιχείων βρίσκουμε εδώ:
14 Πειραματική γεωμετρία
Ενδιαφέροντα ιστορικά στοιχεία για την πειραματική γεωμετρία και την κατασκευή εργαλείων καθώς και για την διδακτική τους αξιοποίηση με μορφή δραστηριοτήτων υπαρχουν εδώ.
15. Μη ευκλείδειες γεωμετρίες
Ο μύθος του Ευκλείδη.
" Η ευκλείδεια γεωμετρία περιέχει τις μόνες αληθινές εποπτείες γιατί ταιριάζει απόλυτα με την εμπειρική μας πραγματικότητα".
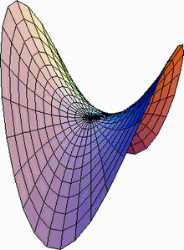
Υπερβολικό παραβολοειδές.
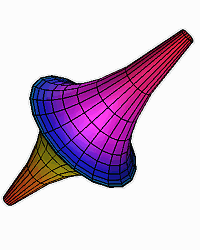
Ψευδοσφαίρα.
" Καμμία γεωμετρία δεν είναι περισσότερο αληθινή. Είναι απλά πιο βολική ".
Ανρί Πουανκαρέ. Γάλλος μαθηματικός
18. IΣΤΟΡΙΑ ΤΟΥ ΠΥΘΑΓΩΡΕΙΟΥ ΘΕΩΡΗΜΑΤΟΣ
Μπορείτε να βρείτε εμπεριστατωμένη ιστορία του πυθαγωρείου θεωρήματος εδώ.
20. Συνοπτική ιστορία των αρχαιοελληνικών μαθηματικών
από το κλασσικό βιβλίο " Σύντομη ιστορία των μαθηματικών " του Dirk J Stuik : εδώ.
22. Η ανθρωπολογία των μαθηματικών
Πολ Έρντος
Θέων ο Αλεξανδρεύς
Θεανώ η Θουρία
Θαλής ο Μιλήσιος
Κωνσταντίνος Καραθεοδωρή
Λ
Άντα Λάβλεϊς
Πιέρ Σιμόν Λαπλάς
Ντάνιελ Μπερνούλι
Τζον Νέπερ
Τζον φον Νόιμαν
Ντεκάρτ
Σαρλ-Εζέν Ντελωναί
Πυθαγόρας ο Σάμιος
Μπλεζ Πασκάλ
Μπέρναρντ Ρίμαν
Φ
Φιμπονάτσι
Ζοζέφ Φουριέ
Κρίστιαν Χόυχενς
Από το μυθιστόρημα : " Το θεώρημα του παπαγάλου " του Ντενί Γκετζ
Η ετυμολογία των μαθηματικών
Μαθηματικά : Εμφανίζεται για πρώτη φορά ως λέξη που δηλώνει μια νέα επιστήμη στην αρχαία Ελλάδα. Προέρχεται από την ελληνική λέξη μάθημα.Πριν τους Έλληνες οι αρχαίοι λαοί όπως οι Αιγύπτιοι , οι Σουμέριοι , οι Κινέζοι κ.α. εκτελούσαν άτυπες μαθηματικές πράξεις με καθαρά χρηστικό και πρακτικό χαρακτήρα.Στην Αίγυπτο π.χ υπήρχαν οι γραφείς που μαζί με όλα τα γραφικά καθήκοντα μετρούσαν την έκταση των αγροτεμαχίων , υπολόγιζαν τους μήνες , έκαναν αστρολογικούς υπολογισμούς , επιλύαν προβλήματα καθημερινής ζωής. Όλα αυτά μέσα σε επαγγεματικά πλαίσια. Έτσι άτυπα έβρισκαν μαθηματικές μεθόδους που όμως περιοριζόταν σε υπολογιστικό χαρακτήρα με πρακτική αξία.Γι' αυτό τα μαθηματικά πριν τους Έλληνες τα θεωρούμε "άτυπα ή ασυνείδητα μαθηματικά"Με τον Θαλή στην αρχαία Ελλάδα εισάγεται η έννοια της απόδειξης και αναζητούνται συμπεράσματα που έχουν καθολική ισχύ και μπορούν να αποδειχτούν.Ο Θαλής θεωρείται ο πατέρας των μαθηματικών ή ο πρώτος μαθηματικός στην Ιστορία τους.Επίσης αναπτύσσονται από τον ίδιο τα αφηρημένα μαθηματικά που κινούνται σε δεύτερο επίπεδο αυτό της μεταγνώσης.Δημιούργησαν δηλαδή αφηρημένες θεωρίες που δεν έχουν υπολογιστική αξία ( θεωρία λόγων , ομοιότητα , ισότητα κ.α.) με την βοήθεια όμως των οποίων επιλύουμε πρακτικά προβλήματα ( μέτρηση του ύψους μιας πυραμίδας , την απόσταση ενός πλοίου από την ακτή κ.α). Επίσης στην αρχαία Ελλάδα εμφανίζονται για πρώτη φορά επαγγεγματίες μαθηματικοί ως μια χωριστή τάξη διανοουμένων που προάγουν την μαθηματική επιστήμη και ιδρύουν σχολές με μαθητές όπου τους διδάσκουν τη νέα επιστήμη : τα μαθηματικά.Ένα ενδιαφέρον παράδειγμα είναι η Πυθαγόρεια σχολή που έβγαλε σημαντικούς μαθηματικούς.Για πολλούς το ελληνικό θαύμα οφείλεται στις καινοτομίες της ελληνικής κοινωνίας όπως η δημοκρατία , το νόμισμα και το αλφάβητο που πρωτοεμφανίζονται τότε.
Άλγεβρα : Προέρχεται από την αραβική λέξη al-jebr που σημαίνει μεταφορά στο άλλο μέλος. Χρωστάει δηλαδή την ονομασία της στην γνωστή διαδικασία της επίλυσης πρωτοβάθμιων εξισώσεων. Στην πραγματικότητα al-jebr σημαίνει στα αραβικά "βάζω στη θέση του κάτι σπασμένο".Οι πρακτικοί ορθοπεδικοί στις μουσουλμανικές χώρες εκείνη την εποχή χτυπούσαν λίγο στα αριστερά και λίγο δεξιά το σπασμένο πόδι μέχρι να έρθει στη θέση του.Μετά το έδεναν με δύο σανίδες πάνω και κάτω.Ο μαθηματικός Χουαρίσμι λοιπόν παρομοίαζε την τεχνική αυτή των ορθοπεδικών με τη διαδικασία επίλυσης μιας εξίσωσης.Μετακινούμε τους γνωστούς και αγνώστους όρους αριστερά και δεξιά μέχρι να έρθει στη θέση του ο άγνωστος και να καταφέρουμε να τον αποκαλύψουμε.Οι δυτικοί έμποροι που είχαν συναλλαγές με τις αραβικές χώρες θαύμασαν τα κείμενα του Χουαρίσμι και τις μεθόδους του και τις έφεραν στην Ευρώπη.Τον 12ο ήδη αιώνα μ.Χ ο Χουαρίσμι ήταν μια διασημότητα στη Δύση.Από την παράφραση λοιπόν του al-jebr που χρησιμοποίησε ο Άραβας μαθηματικός πήρε το όνομά της η άλγεβρα που εγκαινιάστηκε στις αραβικές χώρες και πέρασε στην Ευρώπη.Η άλγεβρα λοιπόν δεν γεννήθηκε στην Ελλάδα, γιατί απλόυστατα γεννήθηκε στη Βαγδάτη! Από τότε άνθισε με τους ευρωπαίους μαθηματικούς. Αρχικά ο Ταρτάλια και ο Cardano επιλύουν με ριζικά την τριτοβάθμια και τεταρτοβάθμια εξίσωση. Κατόπιν ο Abel και ο Γκαλουά αποδεικνύουν ότι οι εξισώσεις ανωτέρου του τετάρτου βαθμού δεν είναι επιλύσιμες με ριζικά. Τον 15ο και 16ο αιώνα εδραιώνεται ο αλγεβρικός λογισμός.Σύμβολα όπως : < , > από τον Τόμας Χάριοτ , = από τον Ρέκορντ , το σύμβολο της ρίζας από τον Ρούντολφ , του απείρου από τον Ουάλις , της δύναμης από τον Σικέ ενδυναμώνουν την άλγεβρα , ως μια χρήσιμη οικουμενική μέθοδο επίλυσης προβλημάτων και μοντελοποίησης της πραγματικότητας.Όταν τον 17ο αιώνα αναπτύσετται η αλγεβροποίση της γεωμετρίας με την ανακάλυψη της αναλυτικής γεωμετρίας από τους Φερμά και Ντεκάρτ αναδεικύεται η αξία της άλγεβρας που μπορεί να υποκαθιστά τη γεωμετρία. Η αρχαιοελληνική εμμονή στη γεωμετρία επηρεασμένη από την πλατωνική ιδεαλιστική αντίληψη υποκαθιστάται από την χρηστική υπεροχή της άλγεβρας στην επίλυση προβλημάτων και στην εφαρμογή στις επιστήμες.Ο νέος κλάδος των μαθηματικών με λίγους αιώνες ζωή παίρνει τη σκυτάλη και της αναγνωρίζεται το προβάδισμα.
Γεωμετρία : Ωφείλει και πάλι την ονομασία της στους Έλληνες. Η μέτρηση της γης κατά κυριολεξία.Η ελληνική αρχαιότητα ήταν επηρεασμένη από την πλατωνική αντίληψη της ανωτερότητας της γεωμετρίας έναντι της αριθμητικής. Για τον Πλάτωνα που πίστευε στην αξία των ιδεών που βοηθούν στην τελείωση της ψυχής και στην αναζήτηση της αρμονίας και της αλήθειας η γεωμετρία ως μια επιστήμη εξαγωγής συμπερασμάτων βοηθούσε σε κατι τέτοιο. Έβλεπε δηλαδή με καλό μάτι την διανοητική ενασχόληση με την θεωρητική γεωμετρία που ακονίζει το νου,ενδυναμώνει τη λογική και αναζητεί τις γεωμετρικές αλήθειες.Η απαίτηση να αναζητούνται γεωμετρικές κατασκευές μόνο με χρήση κανόνα και διαβήτη ήταν πλατωνική άποψη , γιατί έτσι τα μαθηματικά γίνονται ένα εγκεφαλικό παιχνίδι λογικής ανύψωσης του ατόμου.Στα ελληνιστικά χρόνια με πρωτεργάτες τον Αρχιμήδη , τον Ήρωνα , τον Ιππία , τον Πτωλεμαίο κ.α η γεωμετρία χάνει τον θεωρητικό προσανατολισμό της και τον στατικό χαρακτήρα της.Μπαίνει για πρώτη φορά η κίνηση στη γεωμετρία.Σημεία που κινούνται , ευθείες που γλιστρούν και μετατοπίζονται, σχήματα που στρέφονται κ.α. Επίσης χρησιμοποιείται η γεωμετρία σε μηχανικές κατασκευές και έχουμε ένα τεχνολογικό θαύμα εκείνη την εποχή.Κατασκευάζεται η πρώτη ατμομηχανή από τον Ηρωνα , οι πολιορκητικές μηχανές από τον Αρχιμήδη , αστρολάβος από τον Πτολεμαίο κ.α.Η συμβολή της γεωμετρίας με τη νέα οπτική της είναι αξιόλογη.Η αναλυτική γεωμετρία τον 17ο μ.Χ αιώνα όπως προείπαμε ανέδειξε την υπεροχή της άλγεβρας και τα μαθηματικά ξέφυγαν από την μονοκρατορία της γεωμετρίας που στηριζόταν στη επίδραση του Πλάτωνα ανά τους αιώνες.Χωρίς να χάνει την αξία της η γεωμετρία που παραμένει κορωνίδα του μαθηματικού οικοδομήματος δεν μονωπολεί το μαθηματικό γίγνεσθαι.
Σύγχρονα μαθηματικά: Τα μαθηματικά στην Δυτική Ευρώπη μετά τον 12ο αιώνα γνώρισαν μεγάλη άνθιση. Αρχικά αναπτύχθηκε ο νέος κλάδος των μαθηματικών η άλγεβρα.Επιλύθηκαν οι εξισώσεις μέχρι 4ου βαθμού. Αποκορύφωμα στάθηκε η εμφάνιση και στερέωση του αλγεβρικού συμβολισμού τον 15- 16ο αιώνα.Το σημαντικό άλμα αποτέλεσε η ανακάλυψη της αναλυτικής γεωμετρίας τον 17ο αιώνα και η ανακάλυψη του διαφορικού και ολοκληρωτικού λογισμού. Ο Νιούτον και ο Λάιμπνιτς μέσα από διαφορετικούς δρόμους ( ταχύτητα , πρόβλημα εφαπτομένης αντίστοιχα) θεωρούνται οι πρωτεργάτες του νέου κλάδου. Από τότε μελετώνται ποσότητες που πλησιάζουν άλλες χωρίς ποτέ να τις φτάνουν.Ακόμη καμπύλες , ακρότατα , μονοτονία. Υπολόγισαν εμβαδά καμπυλόγραμμμων χωρίων και μήκη καμπυλών με τη βοήθεια του ολοκληρώματος. Σε λίγο η παραγώγιση και η ολοκλήρωση θα γίνουν συνηθισμένες μαθηματικές πράξεις αντίστροφες μεταξύ τους όπως η τετραγωνική ρίζα και το τετράγωνο.Ακόμη στον ίδιο αιώνα πρωτοεμφανίζεται η θεωρία πιθανοτήτων στις επιστολές που αντάλλαξαν ο Φερμά με τον Πασκάλ και μελέτησαν την συνδυαστική.
Από τότε στα 1949 τα μαθηματικά αριθμούν 3400 διαφορετικούς κλάδους και στα σημερικνά χρόνια κυκλοφορούν 200.000 θεωρήματα κάθε χρόνο στα επιστημονικά περιοδικά όλου του κόσμου. Ο " μολυσμός αυτός της σκέψης" όπως αποκαλέστηκε αποκλείει να υπάρχει μαθηματικός που να γνωρίζει όλη αυτή την παραγωγή μαθηματικής πληροφορίας.Ιδανικός μαθηματικός στις μέρες μας δεν είναι αυτός που τα ξέρει όλα , κάτι το αδύνατο , αλλά όποιος έχει την ευφή ιδέα να καινοτομήσει στα μαθηματικά και να τα οδηγήσει σε νέους πρωτότυπους δρόμους.
Σταχυολογήματα από το βιβλίο : "Αρχαία μαθηματικά΄" της S. Cuomo.
O Ηρόδοτος αναφέρει την αρχαιοαιγυπτιακή προέλευση της γεωμετρίας .Έτσι είναι ο πρώτος που αναφέρεται στην ιστορία των μαθηματικών. Συγκεκριμένα αναφέρει ότι ο Ραμψής αποφάσισε να παραχωρήσει σε όλους τους υπηκόους του πανομοιότυπα αγροτεμάχια τετράγωνα και με το ίδιο εμβαδόν. Έτσι όλοι οι υπήκοοι θα έπρεπε να πληρώνουν τον ίδιο φόρο.Όμως κάθε χρόνο οι πλημμύρες του Νείλου κατέστρεφαν κάποια χωράφια , διαβρώνοντας τα τμήματά τους.Ο Ραμψής έστελνε τους γραφείς να μετρήσουν αυτές τις απώλειες σε καλλιεργήσιμη έκταση , ώστε να μειωθεί οι φόρος.Έτσι δημιουργήθηκε η γεωμετρία που αφορούσε τη μέτρηση της γης. Ο Ηρόδοτος μάλιστα λέει : "Όταν διασπάστηκε η ισότητα οι άνθρωποι δημιούργησαν τη γεωμετρία"
Οι Έλληνες μαθηματικοί εισήγαγαν την έρευνα των γενικών θεωρημάτων που έπρεπε να αποδειχθούν με τρόπο ώστε να είναι αντικειμενικά πειστικά.Με άλλα λόγια οι Αιγύπτιοι ήταν ικανοί να υπολογίζουν τον όγκο ενός κυλίνδρου και να βεβαιώνονται ότι το αποτέλεσμα ήταν σωστό ή τουλάχιστον κατάλληλο για τους συγκεκριμένους πρακτικούς σκοπούς τους. Οι Έλληνες βρήκαν τον γενικό τύπο για τον όγκο οποιουδήποτε κυλίνδρου και απέdειξαν ότι είναι σωστός. Οι πολιτικές συνθήκες και η δημόσια ζωή στην Αθήνα εκείνης της εποχής θεωρούντaι ως βασικός παράγοντας για τη δημιουργία αυτής της διαφοράς.
Για τον Πλάτωνα τα μαθηματικά είχαν ιδιαίτερο ενδιαφέρον γιατί αν και ασχολούνται με αισθητά πράγματα αναφέρονται επίσης στο γενικό, στο αφηρημένο και στο αμετάβλητο. Για παράδειγμα μπορεί σε ένα λογαριασμό να ασχολούμαστε με τρία βόδια ή πέντε δάκτυλα αλλά με το "τρία" ή με το "πέντε" έχουμε περιττούς αριθμούς αεξάρτητους από τα αισθητά αντικείμενα.
Ο Πλάτωνας θεωρούσε τα μαθηματικά αντικείμενα ως μοναδικές αληθινές ιδέες.Τα έβλεπε ενδιάμεσα μεταξύ των αισθητών αντικειμένων και των υπερτάτων ιδεών.Γι΄αυτό απέδιδε στην μαθηματική γνώση καθοριστικό ρόλο στην εκπαίδευση των νέων.
Ο ίδιος ο Πλάτων επέκρινε τον Εύδοξο , τον Αρχύτα και τον Μέναιχμο που επιχειρούσαν να μεταθέσουν το πρόβλημα του τετραγωνισμού του κύκλου στον χώρο των ενόργανων και μηχανικών κατασκευών και όχι στη χρήση της λογικής αλλά προσπαθούσαν να το επιλύσουν με οποιοδήποτε δυνατό τρόπο. Την εποχή εκείνη τα μαθηματικά ως λογική δομή συνδεόταν με τη φιλοσοφία και οι φιλόσοφοι είχαν την εποπτεία των μαθηματικών.
Ο Αριστοτέλης δεν θεωρούσε τα μαθηματικά αντικείμενα ως ιδέες του πραγματικού κόσμου αλλά ως αφηρημένες ιδέες που περιγράφουν τα φυσικά αντικείμενα χωρίς να είναι αντικείμενα με αυτοτελή ύπαρξη.Ασχολήθηκε με την λογική δομή των μαθηματικών τα οποία χαρακτήριζε: "έξις αποδεικτική" (αποδεικτική συνήθεια). Eπίσης θεωρούσε ότι αντικείμενο μελέτης των μαθημτικών είναι το "καθ' όλον" κι όχι το "τυχαίο ον". Με τον όρο "καθ' όλον" εννοούσε τα συμπεράσματα που είχαν καθολική ισχύ και αποδεικνυόταν ότι ισχύουν πάντοτε σε όλες τις συνθήκες. Κάτι σαν τους σταθερούς νόμους της φύσης που διέπονται από μια αιτιοκρατία (ντετερμενισμό). "Τυχαίο ον" είναι οτιδήποτε ισχύει τυχαία σε μεμονωμένες και απροσδιόριστες συνθήκες χωρίς να έχει καθολική και αιτιοκρατική ισχύ. Για το Αριστοτέλη τα τυχαία φαινόμενα δεν αποτελούσαν αντικείμενο μελέτης της μαθηματικής επιστήμης.Για το λόγο αυτό η στατιστική και η θεωρία πιθανοτήτων δεν εμφανίστηκαν στα αρχαιοελληνικά μαθηματικά. Βρισκόταν έξω από τα πλαίσια της καθολικότητας και του αποδεικτικού συλλογισμού.
O Aριστοτέλης διαιρεί τη θεωρητική φιλοσοφία σε τρεις βασικές κατηγορίες , τη φυσική , τα μαθηματικά και τη θεολογία. Κατα τόν ίδιο οι δυο πρώτες κατηγορίες πρέπει ονομαστούν εικασίες παρά γνώσεις. Μόνο τα μαθηματικά μπορούν να προσφέρουν ασφαλή και ακλόνητη γνώση σε όσους ασχολούνται μαζί τους , εφ' όσον αυτό γίνεται με επιμονή.
Ένα πό τα σημαντικότερα στοιχεία των ελληνιστικών μαθηματικών είναι ότι επιτέλους έχουμε πλήρεις μαθηματικές πραγματείες αντί για αποσπασματική και έμμεση πληροφόρηση.
Η μέθοδος της "απαγωγής σε άτοπο" αποδίδεται στον Πυθαγόρειο μαθηματικό Ιπποκράτη το Χίο.Είναι αυτός που τετραγώνισε μηνίσκους.Βρήκε δηλαδή τετράγωνα με εμβαδόν ίσο με μηνίσκους. Ήταν ο πρώτος τετραγωνισμός καμπυλόγραμμου σχήματος. Η μέθοδος αυτή γέννησε προσδοκίες για το μεγάλο άλυτο πρόβλημα της αρχαιότητας : τον τετραγωνισμό του κύκλου. Η μέθοδος της απαγωγής σε άτοπο αξιοποιήθηκε από τους Πυθαγόρειους για να αποδείξουν ότι η τετραγωνική ρίζα του 2 δεν είναι ρητός αριθμός.
Ο Ήρωνας ο Αλεξανδρεύς φημίζεται για τη κατασκευή ποικίλων μηχανών.Είναι η εποχή των ελληνιστικών μαθηματικών που παρατηρείται μια στροφή στην σύνδεση της γεωμετρίας με τη μηχανική. Απομακρυνόμαστε από τον θεωρητικό προσανατολισμό των μαθηματικών ιδεών όπως τις θεωρούσε ο Πλάτων. Ο Ήρων στα έργα του (Μηχανικά , Αυτόματα , Περί διόπτρας , Βελοποιικά , Πνευματικά) περιγράφει μηχανές για διάφορους σκοπούς : ανύψωση βαρών , μεγένθυνση τρισδιάστατων αντικειμένων , κόψιμο χοντρών ξύλων, στήριξη στέγης ,δημιουργία κουκλοθέατρου, σβήσιμο φωτιάς με υδραντλία , παραγωγή μουσικής.Ο κρυφός μηχανισμός κουκλοθέατρου κατασκευάζεται βάσει της στερεομετρίας.Η λειτουργία μιας αντλίας εξηγείται μέσω μιας έμμεσης γεωμετρικής απόδειξης. Τα Αυτόματα και τα Πνευματικά περιγράφουν αυτοκινούμενα αγάλματα του Διόνυσου ή απύθμενα κύπελλα από τα οποία αναβλύζει κρασί χωρίς διακοπή. Στο Περί Διόπτρας και στα Μετρικά περιγράφει λεπτομερειακά την κατασκευή μιας διόπτρας και μελετώνται οι πολυάριθμες χρήσεις της στην τοπογραφία , αστρονομία και τη μηχανική.
ή πιο κομψά : "Δεν είναι δυνατόν να αναλύσουμε μια δύναμη ενός ακεραίου σε άθροισμα δύο ίδιων δυνάμεων δύο άλλων ακεραίων ,εκτός αν η δύναμη είναι τετράγωνο".
Ο Φερμά ισχυριζόταν ότι κατείχε μια απόδειξη του συγκεκριμένου θεωρήματος. Η απόδειξη αυτή όμως δεν βρέθηκε ποτέ! Από τότε παρέμενε ένα άλυτο πρόβλημα προς διερεύνηση. Τελικά μόλις στις 23 Ιουνίου του 1993 βρέθηκε η απόδειξη από τον Wiles καθηγητή του Πανεπιστημίου του Princeton της Αγγλίας και ανακοινώθηκε από τον ίδιο σε ένα μαθηματικό συνέδριο στο Πανεπιστήμιο του Cambridge. O Φερμά είχε δίκιο!
Επιστρέφοντας στον Διόφαντο οφείλουμε να συμπληρώσουμε ότι αναφέρει τους αρνητικούς αριθμούς , κάτι που αποτελεί πορωτοπορία για την εποχή του. Επίσης καταλήγει στους γνωστούς κανόνες προσήμων στον πολλαπλασιασμό ρητών αριθμών γράφοντας : "Λείψις επί λείψιν ποιεί ύπαρξιν. Λείψις επί ύπαρξις ποιεί λείψιν". Επίσης στον Διόφαντο βρίσκουμε για πρώτη φορά στην ιστορία των μαθηματικών τη χρήση αλγεβρικού συμβολισμού για την άγνωστη ποσότητα, τις δυνάμεις και τα πολυώνυμα. Ο συμβολισμός του βέβαια δεν είναι αυτός που επικρατεί σήμερα. Θεωρεί την άγνωστη ποσότητα :"ως περιέχουσα απροσδιόριστον ή μη ορισμένο πλήθος μονάδων". Την συμβολίζει με ς που αποτελεί το τελευταίο γράμμα της λέξης αριθμός.Γι' αυτό και ο αλγεβρικός συμβολισμός του χαρακτηρίζεται ως συντομογραφικός.
Από το βιβλίο : "Αρχαία μαθηματικά΄" της S. Cuomo.
" Η ύπαρξη της ανυπαρξίας ήταν μια μεγάλη λογική αντίφαση ".
Για το μηδέν.
" Ξυνόν γαρ αρχή και πέρας επι κύκλου περιφερείας".
Δηλαδή : Σε κάθε κύκλο κάθε σημείο του είναι αρχή και τέλος.
Ηράκλειτος. Ίωνας φιλόσοφος. 544 - 684 π.Χ
" Λέγεται ότι το σύμβολο του μηδενός εφευρέθηκε στην Δυτική Ευρώπη όταν κάποιος παρακολουθούσε έναν γλάρο στον ουρανό να κάνει κύκλους και έτσι να παραμένει πάντα στο ίδιο σημείο που ξεκίνησε. Το μηδέν λοιπόν από τότε συμβολίζεται με έναν κύκλο σύμβολο της αέναης κίνησης στο ίδιο σημείο , στο πουθενά και στο τίποτα".
Η ετυμολογία των μαθηματικών
Μαθηματικά : Εμφανίζεται για πρώτη φορά ως λέξη που δηλώνει μια νέα επιστήμη στην αρχαία Ελλάδα. Προέρχεται από την ελληνική λέξη μάθημα.Πριν τους Έλληνες οι αρχαίοι λαοί όπως οι Αιγύπτιοι , οι Σουμέριοι , οι Κινέζοι κ.α. εκτελούσαν άτυπες μαθηματικές πράξεις με καθαρά χρηστικό και πρακτικό χαρακτήρα.Στην Αίγυπτο π.χ υπήρχαν οι γραφείς που μαζί με όλα τα γραφικά καθήκοντα μετρούσαν την έκταση των αγροτεμαχίων , υπολόγιζαν τους μήνες , έκαναν αστρολογικούς υπολογισμούς , επιλύαν προβλήματα καθημερινής ζωής. Όλα αυτά μέσα σε επαγγεματικά πλαίσια. Έτσι άτυπα έβρισκαν μαθηματικές μεθόδους που όμως περιοριζόταν σε υπολογιστικό χαρακτήρα με πρακτική αξία.Γι' αυτό τα μαθηματικά πριν τους Έλληνες τα θεωρούμε "άτυπα ή ασυνείδητα μαθηματικά"Με τον Θαλή στην αρχαία Ελλάδα εισάγεται η έννοια της απόδειξης και αναζητούνται συμπεράσματα που έχουν καθολική ισχύ και μπορούν να αποδειχτούν.Ο Θαλής θεωρείται ο πατέρας των μαθηματικών ή ο πρώτος μαθηματικός στην Ιστορία τους.Επίσης αναπτύσσονται από τον ίδιο τα αφηρημένα μαθηματικά που κινούνται σε δεύτερο επίπεδο αυτό της μεταγνώσης.Δημιούργησαν δηλαδή αφηρημένες θεωρίες που δεν έχουν υπολογιστική αξία ( θεωρία λόγων , ομοιότητα , ισότητα κ.α.) με την βοήθεια όμως των οποίων επιλύουμε πρακτικά προβλήματα ( μέτρηση του ύψους μιας πυραμίδας , την απόσταση ενός πλοίου από την ακτή κ.α). Επίσης στην αρχαία Ελλάδα εμφανίζονται για πρώτη φορά επαγγεγματίες μαθηματικοί ως μια χωριστή τάξη διανοουμένων που προάγουν την μαθηματική επιστήμη και ιδρύουν σχολές με μαθητές όπου τους διδάσκουν τη νέα επιστήμη : τα μαθηματικά.Ένα ενδιαφέρον παράδειγμα είναι η Πυθαγόρεια σχολή που έβγαλε σημαντικούς μαθηματικούς.Για πολλούς το ελληνικό θαύμα οφείλεται στις καινοτομίες της ελληνικής κοινωνίας όπως η δημοκρατία , το νόμισμα και το αλφάβητο που πρωτοεμφανίζονται τότε.
Άλγεβρα : Προέρχεται από την αραβική λέξη al-jebr που σημαίνει μεταφορά στο άλλο μέλος. Χρωστάει δηλαδή την ονομασία της στην γνωστή διαδικασία της επίλυσης πρωτοβάθμιων εξισώσεων. Στην πραγματικότητα al-jebr σημαίνει στα αραβικά "βάζω στη θέση του κάτι σπασμένο".Οι πρακτικοί ορθοπεδικοί στις μουσουλμανικές χώρες εκείνη την εποχή χτυπούσαν λίγο στα αριστερά και λίγο δεξιά το σπασμένο πόδι μέχρι να έρθει στη θέση του.Μετά το έδεναν με δύο σανίδες πάνω και κάτω.Ο μαθηματικός Χουαρίσμι λοιπόν παρομοίαζε την τεχνική αυτή των ορθοπεδικών με τη διαδικασία επίλυσης μιας εξίσωσης.Μετακινούμε τους γνωστούς και αγνώστους όρους αριστερά και δεξιά μέχρι να έρθει στη θέση του ο άγνωστος και να καταφέρουμε να τον αποκαλύψουμε.Οι δυτικοί έμποροι που είχαν συναλλαγές με τις αραβικές χώρες θαύμασαν τα κείμενα του Χουαρίσμι και τις μεθόδους του και τις έφεραν στην Ευρώπη.Τον 12ο ήδη αιώνα μ.Χ ο Χουαρίσμι ήταν μια διασημότητα στη Δύση.Από την παράφραση λοιπόν του al-jebr που χρησιμοποίησε ο Άραβας μαθηματικός πήρε το όνομά της η άλγεβρα που εγκαινιάστηκε στις αραβικές χώρες και πέρασε στην Ευρώπη.Η άλγεβρα λοιπόν δεν γεννήθηκε στην Ελλάδα, γιατί απλόυστατα γεννήθηκε στη Βαγδάτη! Από τότε άνθισε με τους ευρωπαίους μαθηματικούς. Αρχικά ο Ταρτάλια και ο Cardano επιλύουν με ριζικά την τριτοβάθμια και τεταρτοβάθμια εξίσωση. Κατόπιν ο Abel και ο Γκαλουά αποδεικνύουν ότι οι εξισώσεις ανωτέρου του τετάρτου βαθμού δεν είναι επιλύσιμες με ριζικά. Τον 15ο και 16ο αιώνα εδραιώνεται ο αλγεβρικός λογισμός.Σύμβολα όπως : < , > από τον Τόμας Χάριοτ , = από τον Ρέκορντ , το σύμβολο της ρίζας από τον Ρούντολφ , του απείρου από τον Ουάλις , της δύναμης από τον Σικέ ενδυναμώνουν την άλγεβρα , ως μια χρήσιμη οικουμενική μέθοδο επίλυσης προβλημάτων και μοντελοποίησης της πραγματικότητας.Όταν τον 17ο αιώνα αναπτύσετται η αλγεβροποίση της γεωμετρίας με την ανακάλυψη της αναλυτικής γεωμετρίας από τους Φερμά και Ντεκάρτ αναδεικύεται η αξία της άλγεβρας που μπορεί να υποκαθιστά τη γεωμετρία. Η αρχαιοελληνική εμμονή στη γεωμετρία επηρεασμένη από την πλατωνική ιδεαλιστική αντίληψη υποκαθιστάται από την χρηστική υπεροχή της άλγεβρας στην επίλυση προβλημάτων και στην εφαρμογή στις επιστήμες.Ο νέος κλάδος των μαθηματικών με λίγους αιώνες ζωή παίρνει τη σκυτάλη και της αναγνωρίζεται το προβάδισμα.
Σύγχρονα μαθηματικά: Τα μαθηματικά στην Δυτική Ευρώπη μετά τον 12ο αιώνα γνώρισαν μεγάλη άνθιση. Αρχικά αναπτύχθηκε ο νέος κλάδος των μαθηματικών η άλγεβρα.Επιλύθηκαν οι εξισώσεις μέχρι 4ου βαθμού. Αποκορύφωμα στάθηκε η εμφάνιση και στερέωση του αλγεβρικού συμβολισμού τον 15- 16ο αιώνα.Το σημαντικό άλμα αποτέλεσε η ανακάλυψη της αναλυτικής γεωμετρίας τον 17ο αιώνα και η ανακάλυψη του διαφορικού και ολοκληρωτικού λογισμού. Ο Νιούτον και ο Λάιμπνιτς μέσα από διαφορετικούς δρόμους ( ταχύτητα , πρόβλημα εφαπτομένης αντίστοιχα) θεωρούνται οι πρωτεργάτες του νέου κλάδου. Από τότε μελετώνται ποσότητες που πλησιάζουν άλλες χωρίς ποτέ να τις φτάνουν.Ακόμη καμπύλες , ακρότατα , μονοτονία. Υπολόγισαν εμβαδά καμπυλόγραμμμων χωρίων και μήκη καμπυλών με τη βοήθεια του ολοκληρώματος. Σε λίγο η παραγώγιση και η ολοκλήρωση θα γίνουν συνηθισμένες μαθηματικές πράξεις αντίστροφες μεταξύ τους όπως η τετραγωνική ρίζα και το τετράγωνο.Ακόμη στον ίδιο αιώνα πρωτοεμφανίζεται η θεωρία πιθανοτήτων στις επιστολές που αντάλλαξαν ο Φερμά με τον Πασκάλ και μελέτησαν την συνδυαστική.
Από τότε στα 1949 τα μαθηματικά αριθμούν 3400 διαφορετικούς κλάδους και στα σημερικνά χρόνια κυκλοφορούν 200.000 θεωρήματα κάθε χρόνο στα επιστημονικά περιοδικά όλου του κόσμου. Ο " μολυσμός αυτός της σκέψης" όπως αποκαλέστηκε αποκλείει να υπάρχει μαθηματικός που να γνωρίζει όλη αυτή την παραγωγή μαθηματικής πληροφορίας.Ιδανικός μαθηματικός στις μέρες μας δεν είναι αυτός που τα ξέρει όλα , κάτι το αδύνατο , αλλά όποιος έχει την ευφή ιδέα να καινοτομήσει στα μαθηματικά και να τα οδηγήσει σε νέους πρωτότυπους δρόμους.
Σταχυολογήματα από το βιβλίο : "Αρχαία μαθηματικά΄" της S. Cuomo.
Για τον Πλάτωνα τα μαθηματικά είχαν ιδιαίτερο ενδιαφέρον γιατί αν και ασχολούνται με αισθητά πράγματα αναφέρονται επίσης στο γενικό, στο αφηρημένο και στο αμετάβλητο. Για παράδειγμα μπορεί σε ένα λογαριασμό να ασχολούμαστε με τρία βόδια ή πέντε δάκτυλα αλλά με το "τρία" ή με το "πέντε" έχουμε περιττούς αριθμούς αεξάρτητους από τα αισθητά αντικείμενα.
Ο Πλάτωνας θεωρούσε τα μαθηματικά αντικείμενα ως μοναδικές αληθινές ιδέες.Τα έβλεπε ενδιάμεσα μεταξύ των αισθητών αντικειμένων και των υπερτάτων ιδεών.Γι΄αυτό απέδιδε στην μαθηματική γνώση καθοριστικό ρόλο στην εκπαίδευση των νέων.
Ο ίδιος ο Πλάτων επέκρινε τον Εύδοξο , τον Αρχύτα και τον Μέναιχμο που επιχειρούσαν να μεταθέσουν το πρόβλημα του τετραγωνισμού του κύκλου στον χώρο των ενόργανων και μηχανικών κατασκευών και όχι στη χρήση της λογικής αλλά προσπαθούσαν να το επιλύσουν με οποιοδήποτε δυνατό τρόπο. Την εποχή εκείνη τα μαθηματικά ως λογική δομή συνδεόταν με τη φιλοσοφία και οι φιλόσοφοι είχαν την εποπτεία των μαθηματικών.
Ο Αριστοτέλης δεν θεωρούσε τα μαθηματικά αντικείμενα ως ιδέες του πραγματικού κόσμου αλλά ως αφηρημένες ιδέες που περιγράφουν τα φυσικά αντικείμενα χωρίς να είναι αντικείμενα με αυτοτελή ύπαρξη.Ασχολήθηκε με την λογική δομή των μαθηματικών τα οποία χαρακτήριζε: "έξις αποδεικτική" (αποδεικτική συνήθεια). Eπίσης θεωρούσε ότι αντικείμενο μελέτης των μαθημτικών είναι το "καθ' όλον" κι όχι το "τυχαίο ον". Με τον όρο "καθ' όλον" εννοούσε τα συμπεράσματα που είχαν καθολική ισχύ και αποδεικνυόταν ότι ισχύουν πάντοτε σε όλες τις συνθήκες. Κάτι σαν τους σταθερούς νόμους της φύσης που διέπονται από μια αιτιοκρατία (ντετερμενισμό). "Τυχαίο ον" είναι οτιδήποτε ισχύει τυχαία σε μεμονωμένες και απροσδιόριστες συνθήκες χωρίς να έχει καθολική και αιτιοκρατική ισχύ. Για το Αριστοτέλη τα τυχαία φαινόμενα δεν αποτελούσαν αντικείμενο μελέτης της μαθηματικής επιστήμης.Για το λόγο αυτό η στατιστική και η θεωρία πιθανοτήτων δεν εμφανίστηκαν στα αρχαιοελληνικά μαθηματικά. Βρισκόταν έξω από τα πλαίσια της καθολικότητας και του αποδεικτικού συλλογισμού.
O Aριστοτέλης διαιρεί τη θεωρητική φιλοσοφία σε τρεις βασικές κατηγορίες , τη φυσική , τα μαθηματικά και τη θεολογία. Κατα τόν ίδιο οι δυο πρώτες κατηγορίες πρέπει ονομαστούν εικασίες παρά γνώσεις. Μόνο τα μαθηματικά μπορούν να προσφέρουν ασφαλή και ακλόνητη γνώση σε όσους ασχολούνται μαζί τους , εφ' όσον αυτό γίνεται με επιμονή.
Ένα πό τα σημαντικότερα στοιχεία των ελληνιστικών μαθηματικών είναι ότι επιτέλους έχουμε πλήρεις μαθηματικές πραγματείες αντί για αποσπασματική και έμμεση πληροφόρηση.
Η μέθοδος της "απαγωγής σε άτοπο" αποδίδεται στον Πυθαγόρειο μαθηματικό Ιπποκράτη το Χίο.Είναι αυτός που τετραγώνισε μηνίσκους.Βρήκε δηλαδή τετράγωνα με εμβαδόν ίσο με μηνίσκους. Ήταν ο πρώτος τετραγωνισμός καμπυλόγραμμου σχήματος. Η μέθοδος αυτή γέννησε προσδοκίες για το μεγάλο άλυτο πρόβλημα της αρχαιότητας : τον τετραγωνισμό του κύκλου. Η μέθοδος της απαγωγής σε άτοπο αξιοποιήθηκε από τους Πυθαγόρειους για να αποδείξουν ότι η τετραγωνική ρίζα του 2 δεν είναι ρητός αριθμός.
Ο Ήρωνας ο Αλεξανδρεύς φημίζεται για τη κατασκευή ποικίλων μηχανών.Είναι η εποχή των ελληνιστικών μαθηματικών που παρατηρείται μια στροφή στην σύνδεση της γεωμετρίας με τη μηχανική. Απομακρυνόμαστε από τον θεωρητικό προσανατολισμό των μαθηματικών ιδεών όπως τις θεωρούσε ο Πλάτων. Ο Ήρων στα έργα του (Μηχανικά , Αυτόματα , Περί διόπτρας , Βελοποιικά , Πνευματικά) περιγράφει μηχανές για διάφορους σκοπούς : ανύψωση βαρών , μεγένθυνση τρισδιάστατων αντικειμένων , κόψιμο χοντρών ξύλων, στήριξη στέγης ,δημιουργία κουκλοθέατρου, σβήσιμο φωτιάς με υδραντλία , παραγωγή μουσικής.Ο κρυφός μηχανισμός κουκλοθέατρου κατασκευάζεται βάσει της στερεομετρίας.Η λειτουργία μιας αντλίας εξηγείται μέσω μιας έμμεσης γεωμετρικής απόδειξης. Τα Αυτόματα και τα Πνευματικά περιγράφουν αυτοκινούμενα αγάλματα του Διόνυσου ή απύθμενα κύπελλα από τα οποία αναβλύζει κρασί χωρίς διακοπή. Στο Περί Διόπτρας και στα Μετρικά περιγράφει λεπτομερειακά την κατασκευή μιας διόπτρας και μελετώνται οι πολυάριθμες χρήσεις της στην τοπογραφία , αστρονομία και τη μηχανική.
Ο Ήρωνας στο έργο του "Μετρικά" λέει : "οι παλιές περιγραφές μας διδάσκουν ότι η γεωμετρία ασχολείται με τη μέτρηση και διαίρεση της γης". Στην εποχή του η γεωμετρία καινοτομεί και συνδέται με τη μηχανική με θαυμαστά αποτελέσματα. Σε άλλο σημείο αποφαίνεται : " Σε ένα τέτοιο κόσμο η απόλυτη ακρίβεια δεν είναι δυνατή και συχνά πρέπει να αρκεστούμε στην καλύτερη προσέγγιση".
Ο Ήρωνας με εριστική διάθεση στο έργο του Βελοποιικά δημιουργεί το πλαίσιο ανταγωνισμού μεταξύ της φιλοσοφίας και της μηχανικής.Η φιλοσοφία , ισχυρίζεται, χρησιμοποιεί συλλογισμούς οι οποίοι είναι απλές λέξεις ενώ η μηχανική μηχανές που μπορούμε να τις αγγίξουμε.
Ο Διόφαντος θεωρείται από πολλoύς ο δημιουργός της άλγεβρας και συνεπώς βρίσκεται μπροστά από την εποχή του.Το έργο του "Αριθμητικά" δεν έχει λογική - συμπερασματική δομή.Ασχολείται με επίλυση συγκεκριμένων προβλημάτων. Επίσης ταξινομεί και οργανώνει τα προβλήματα και ομαδοποιεί προβλήματα με σαφή ομοιότητα στη σκέψη.Προάγει αυτό που ονομάζουμε αναλογική σκέψη στην επίλυση προβλημάτων. Σημαντικές καινοτομίες του Διόφαντου που δικαιολογούν την άποψη ότι ήταν μπροστά από την εποχή του ήταν οι ακόλουθες. Μελετά τις ακέραιες λύσεις εξισώσεων που ακόμη κια σήμερα φέρουν το όνομά του : "διοφαντικές εξισώσεις".
Επηρεασμένος από αυτόν , το έργο του οποίου μελέτησε , ο Φερμά τον 17ο αιώνα συνεχίζει το έργο του και διατυπώνει αρκετά θεωρήματα για τις ακέραιες λύσεις εξισώσεων. Σε αυτόν τον προβληματισμό ανήκει και το λεγόμενο τελευταίο θεώρημα του Φερμά που διατυπώνεται ως εξής :
Δεν υπάρχουν μη μηδενικές λύσεις (τριάδες) για μια οικογένεια παρόμοιων εξισώσεων της μορφής an+bn=cn , όπου n= ακέραιος >2.Ο Ήρωνας με εριστική διάθεση στο έργο του Βελοποιικά δημιουργεί το πλαίσιο ανταγωνισμού μεταξύ της φιλοσοφίας και της μηχανικής.Η φιλοσοφία , ισχυρίζεται, χρησιμοποιεί συλλογισμούς οι οποίοι είναι απλές λέξεις ενώ η μηχανική μηχανές που μπορούμε να τις αγγίξουμε.
Ο Διόφαντος θεωρείται από πολλoύς ο δημιουργός της άλγεβρας και συνεπώς βρίσκεται μπροστά από την εποχή του.Το έργο του "Αριθμητικά" δεν έχει λογική - συμπερασματική δομή.Ασχολείται με επίλυση συγκεκριμένων προβλημάτων. Επίσης ταξινομεί και οργανώνει τα προβλήματα και ομαδοποιεί προβλήματα με σαφή ομοιότητα στη σκέψη.Προάγει αυτό που ονομάζουμε αναλογική σκέψη στην επίλυση προβλημάτων. Σημαντικές καινοτομίες του Διόφαντου που δικαιολογούν την άποψη ότι ήταν μπροστά από την εποχή του ήταν οι ακόλουθες. Μελετά τις ακέραιες λύσεις εξισώσεων που ακόμη κια σήμερα φέρουν το όνομά του : "διοφαντικές εξισώσεις".
Επηρεασμένος από αυτόν , το έργο του οποίου μελέτησε , ο Φερμά τον 17ο αιώνα συνεχίζει το έργο του και διατυπώνει αρκετά θεωρήματα για τις ακέραιες λύσεις εξισώσεων. Σε αυτόν τον προβληματισμό ανήκει και το λεγόμενο τελευταίο θεώρημα του Φερμά που διατυπώνεται ως εξής :
ή πιο κομψά : "Δεν είναι δυνατόν να αναλύσουμε μια δύναμη ενός ακεραίου σε άθροισμα δύο ίδιων δυνάμεων δύο άλλων ακεραίων ,εκτός αν η δύναμη είναι τετράγωνο".
Ο Φερμά ισχυριζόταν ότι κατείχε μια απόδειξη του συγκεκριμένου θεωρήματος. Η απόδειξη αυτή όμως δεν βρέθηκε ποτέ! Από τότε παρέμενε ένα άλυτο πρόβλημα προς διερεύνηση. Τελικά μόλις στις 23 Ιουνίου του 1993 βρέθηκε η απόδειξη από τον Wiles καθηγητή του Πανεπιστημίου του Princeton της Αγγλίας και ανακοινώθηκε από τον ίδιο σε ένα μαθηματικό συνέδριο στο Πανεπιστήμιο του Cambridge. O Φερμά είχε δίκιο!
Επιστρέφοντας στον Διόφαντο οφείλουμε να συμπληρώσουμε ότι αναφέρει τους αρνητικούς αριθμούς , κάτι που αποτελεί πορωτοπορία για την εποχή του. Επίσης καταλήγει στους γνωστούς κανόνες προσήμων στον πολλαπλασιασμό ρητών αριθμών γράφοντας : "Λείψις επί λείψιν ποιεί ύπαρξιν. Λείψις επί ύπαρξις ποιεί λείψιν". Επίσης στον Διόφαντο βρίσκουμε για πρώτη φορά στην ιστορία των μαθηματικών τη χρήση αλγεβρικού συμβολισμού για την άγνωστη ποσότητα, τις δυνάμεις και τα πολυώνυμα. Ο συμβολισμός του βέβαια δεν είναι αυτός που επικρατεί σήμερα. Θεωρεί την άγνωστη ποσότητα :"ως περιέχουσα απροσδιόριστον ή μη ορισμένο πλήθος μονάδων". Την συμβολίζει με ς που αποτελεί το τελευταίο γράμμα της λέξης αριθμός.Γι' αυτό και ο αλγεβρικός συμβολισμός του χαρακτηρίζεται ως συντομογραφικός.
" Η ύπαρξη της ανυπαρξίας ήταν μια μεγάλη λογική αντίφαση ".
Για το μηδέν.
" Ξυνόν γαρ αρχή και πέρας επι κύκλου περιφερείας".
Δηλαδή : Σε κάθε κύκλο κάθε σημείο του είναι αρχή και τέλος.
Ηράκλειτος. Ίωνας φιλόσοφος. 544 - 684 π.Χ
" Λέγεται ότι το σύμβολο του μηδενός εφευρέθηκε στην Δυτική Ευρώπη όταν κάποιος παρακολουθούσε έναν γλάρο στον ουρανό να κάνει κύκλους και έτσι να παραμένει πάντα στο ίδιο σημείο που ξεκίνησε. Το μηδέν λοιπόν από τότε συμβολίζεται με έναν κύκλο σύμβολο της αέναης κίνησης στο ίδιο σημείο , στο πουθενά και στο τίποτα".
" Ο τροφοσυλέκτης άνθρωπος όταν έγινε κτηνοτρόφος πρώτα έμαθε να αντιστοιχεί και μετά να μετράει. Αντιστοιχούσε σε κάθε ζώο που εξημέρωσε ένα πετραδάκι. 'Οσα ζώα είχε τόσα ήταν και τα πετραδάκια. Στο έδαφος έσκαψε μια λακούβα. Το πρωί έβγαζε τα ζώα να βοσκήσουν. Το βράδυ για κάθε ζώο που έβαζε μέσα στον περιφραγμένο χώρο, έβαζε συγχρόνως και ένα πετραδάκι στη λακούβα. Αν στο τέλος έμενε ένα τουλάχιστον πετραδάκι εκτός σήμαινε ότι κάποιο ζώο έλειπε! ".
" Ένας νάνος στο ψηλότερο σκαλί είναι πιο ψηλά από ένα γίγαντα στο χαμηλότερο". Τι σχέση μπορεί να έχει η παραπάνω φράση με τα μαθηματικά; Έστω ο αριθμός 149. Το ψηφίο 1 είναι νάνος σχετικά με τον μεγαλύτερό του τον γίγαντα 9. Κι όμως το ένα είναι ψηλότερα , έχει μεγαλύτερη αξία από το 9 στον προηγούμενο αριθμό. Αυτό συμβαίνει γιατί βρίσκεται σε ψηλότερο σκαλί ( στο σκαλί των εκατοντάδων) από το χαμηλότερο που βρίσκεται το 9 (στο σκαλί των μονάδων). Η φράση αυτή λοιπόν αναφέρεται στο θεσιακό σύστημα αρίθμησης. Οι Ευρωπαίοι έμποροι βρήκαν αυτό το αριθμητικό σύστημα στους Άραβες και εντυπωσιάστηκαν. Το μετέφεραν αμέσως στη Δύση και από τοτε επικράτησε παγκοσμίως.Σήμεμα το αποκαλούμε αραβικό σύστημα αρίθμησης. Το σωστότερο βέβαια θα ήταν να το αποκαλούσαμε ινδοαραβικό. Κι αυτό γιατί λησμονούμε ότι οι Άραβες το δανείστηκαν από τους Ινδούς. Οι Ινδοί λοιπόν ανακάλυψαν και πρωτοχρησιμοποίησαν το θεσιακό σύστημα αρίθμησης. Ας σκεφτούμε τώρα τι σημαίνει η φράση : " Η αξία εξαρτάται από τη θέση". Τι σημαίνει άραγε για την αξία ενός ανθρώπου στην κοινωνία αλλά και για την αξία ενός ψηφίου ανάλογα με τη θέση του σε ένα αριθμό;
" Τον προσδιορισμό της θέσης ενός σημείου με τη χρήση συντεταγμένων την οφείλουμε στον Ντεκάρτ ( Καρτέσιο). Λέγεται ότι βρισκόταν ξαπλωμένος στο κρεβάτι του και παρατηρούσε μια μίγα που πετούσε διαρκώς πάνω από το κεφάλι του. Του γεννήθηκε ο προβληματισμός να προσδιορίσει την θέση της , μια και άλλαζε συνέχεια. Διαπίστωσε ότι του χρειαζόταν τρεις αριθμοί. Ένας για την απόσταση της από το ταβάνι και δύο ακόμη για τις αποστάσεις της από δύο πλαϊνούς τοίχους. Επρόκειτο για την πρώτη σύλληψη των τριών συνταταγμένων σημείου του χώρου".
" H πιο αιμοβαμμένη θεωρία στα μαθηματικά είναι σίγουρα η θεωρία ομάδων του Galois. Μονομάχησε με δύο φίλους της αγαπημένης του Stephanie. Η μονομαχία κατέληξε με το θάνατό του στα 21 του χρόνια. Σε γράμμα που απέστειλε νωρίτερα στον φίλο του Auguste Chevalier ο οποίος είχε στην κατοχή του χειρόγραφα της εργασίας του έγραφε :
Tα τρία άλυτα προβλήματα της αρχαιότητας! Διπλασιασμός του κύβου , τριχοτόμηση γωνίας , τετραγωνισμός κύκλου. Όλα τα προβλήματα αυτά ξεκίνησαν ως γενίκευση κάποιων άλλων που είχαν επιλυθεί.
Τετραγωνισμός κύκλου. Να κατασκευαστεί δηλαδή με κανόνα και διαβήτη τετράγωνο που να να έχει εμβαδόν ίσο με δοθέντα κύκλο. Ο Ιπποκράτης ο Χίος κατάφερε να τετραγωνίσει μηνίσκους. Σε μια εποχή που ο τετραγωνισμός αφορούσε ευθύγραμμα σχήματα όπως ορθογώνια , παραλληλόγραμμα και τραπέζια , ο Ιπποκράτης τετραγώνισε καμπυλόγραμμο σχήμα. Γέννησε ξαφνικά τρελές ελπίδες για τον τετραγωνισμό του κύκλου. Αφού οι μηνίσκοι τετραγωνίζονται γιατί όχι και ο κύκλος;
Διπλασιασμός του κύβου. Να κατασκευαστεί με κανόνα και διαβήτη κύβος με διπλάσιο όγκο από ένα δοθέντα κύβο. Το πρόβλημα αυτό είναι γενίκευση του διπλασιασμού τετραγώνου : " Να κατασκευαστεί τετράγωνο με εμβαδόν διπλάσιο από ένα δοθέντα". Η λύση αυτού του προβλήματος είναι να κατασκευάσουμε τετράγωνο με πλευρά τη διαγώνιο του αρχικού τετραγώνου. Το νέο τετράγωνο έχει διπλάσιο εμβαδόν από το αρχικό.
Τριχοτόμηση γωνίας. Το πρόβλημα αυτό αποτελεί γενίκευση της τριχοτόμησης ευθύγραμμου τμήματος. Να χωριστεί δηλαδή ένα ευθύγραμμο τμήμα σε τρία ίσα μέρη. Η κατασκευή αυτή οφείλεται στον Θαλή με χρήση μιας βοηθητικής ημιευθείας και παράλληλων ευθειών. Επεκτάθηκε το πρόβλημα αυτό στην αναζήτηση δύο ημιευθειών που χωρίζουν μια γωνία σε τρία ίσα μέρη. Αφού το ευθύγραμμο τμήμα τριχοτομείται γιατί όχι και η γωνία;
Την εποχή εκείνη οι Έλληνες και οι Αιγύπτιοι πίστευαν ότι όλα τα προβλήματα έχουν λύση. Δεν μπορούσαν να φανταστούν ότι υπάρχουν προβλήματα άλυτα και ακόμη περισσότερο ότι μπορούμε να αποδείξουμε το αδύνατο της λύσης τους. Αργότερα λοιπόν αποδείχθηκε ότι η τριχοτόμηση μιας γωνίας , ο διπλασιασμός του κύβου και ο τετραγωνισμός του κύκλου με κανόνα διαβήτη ανήκουν στην κατηγορία των άλυτων προβλημάτων . Είναι άλυτα όχι γιατί εμείς δεν μπορούμε να τα επιλύσουμε όπως νόμιζαν οι αρχαίοι , αλλά γιατί αποδείχθηκε με σαφή τρόπο ότι είναι αδύνατο να λυθούν.
Το αδύνατο αυτών των κατασκευών στηρίχθηκε στην διαπίστωση ότι όλες αυτές οι γεωμετρικές κατασκευές συνδέονται με άρρητους αριθμούς που δεν είναι αλγεβρικοί αλλά υπερβατικοί. Αλγεβρικοί είναι εκείνοι οι άρρητοι που αποτελούν ρίζες μιας εξίσωσης με ακέραιους συντελεστές. Ο ρίζα 2 για παράδειγμα είναι αλγεβρικός γιατί είναι ρίζα της εξίσωσης: χ2 -2 =0. Ο π όμως είναι υπεβατικός γιατί δεν υπάρχει εξίσωση με ακέραιους συντελεστές που να έχει ρίζα το π. Ο τετραγωνισμός λοιπόν του κύκλου με κανόνα και διαβήτη είναι αδύνατος γιατί ο αριθμός π δεν είναι αλγεβρικός!
Οι πίνακες των χορδών από τον Ίππαρχο και τον Πτολεμαίο είναι τα πρώτα παραδείγματα συναρτήσεων στην ιστορία των μαθηματικών. Τριγωνομετρικών συναρτήσεων.Αργότερα οι Ινδοί αντικατέστησαν τους πίνακες χορδών με πίνακες ημιτόνων, που ήταν πιο εύχρηστοι.Το ημίτονο δεν είναι τίποτα άλλο από το μισό μιας χορδής ενός μοναδιαίου κύκλου. Η λέξη προέρχεται από το σανσκριτικό ζίβα που μεταφράζει την ελληνική έκφραση "χορδή τόξου" που χρησιμοποίησε ο Ίππαρχος. Στα αραβικά έγινε τζίμπα και στα λατινικά sinus. Ο πρώτος μαθηματικός που συνέταξε πίνακες ημιτόνων κι όχι χορδών ήταν ο Άραβας Αλ - Χουαρίσμι.Ο Αλ - Χασίμπ δημιούργησε τις εφαπτομένες. Ο Θαλής θα υπολόγιζε κατευθείαν το ύψος της πυραμίδας του Χέοπα αν διέθετε πίνακες εφαπτομένων. Δεν διέθετε όμως ... Γι' αυτό στηρίχθηκε στην θεωρία ομοιότητας.
Μια μέρα του 1742 ο μαθηματικός Κρίστιαν Γκόλντμπαχ έστειλε μια επιστολή στον Όιλερ , όπου έγραφε : "Κάθε άρτιος αριθμός διαφορετικός του 2 μπορεί να γραφεί ως άθροισμα δύο πρώτων αριθμών. Για παράδειγμα : 16 = 13 + 3 , 30 = 23 + 7". Πέρασαν δυόμισι αιώνες από τότε και εξακολουθούμε να μη γνωρίζουμε αν αυτή πρόταση , γνωστή ως εικασία του Γκόλντμπαχ , είναι αληθής.
Ένα σημείο Μ του επιπέδου με σαφή γεωμετρική υπόσταση μεταμορφώνεται με το μαγικό ραβδί των Φερμά και Ντεκάρτ σε ένα ζευγάρι αριθμών. Ακατα μακατα .... και το σημείο έγινε (x,y).Είναι μια πραγματική επανάσταση! Το γεωμετρικό σημείο πήρε αλγεβρική μορφή. Η καθαρή γεωμετρία έχει πια εξοβελιστεί. Το ίδιο συμβαίνει με τις γεωμετρικές καμπύλες. Η εξίσωσή τους γίνεται το αλγεβρικό τους όνομα!
Το σύμβολο"= " της ισότητας οφείλεται στον μαθηματικό και γιατρό Ρέκορντ στα 1557. Το "x" του πολλαπλασιασμού είναι επινόηση του Άγγλου Ουίλλιαμ Ούγκρεντ στα 1631.Τα σύμβολα "<" , ">" επινόηση του Άγγλου Τομας Χάρριοτ.Το σύμβολο της τετραγωνικής ρίζας από τον Γερμανό Ρούντολφ στα 1525. Το σύμβολο του απείρου από τον Άγγλο Τζον Ουάλλις. Ο συμβολισμός των δυνάμεων από τον Γάλλο Νικολά Συκέ τον 15ο αιώνα. Ο Ντεκάρτ τέλος συμβόλιζε με τα αρχικά μικρά γράμματα της αγγλικής αλφαβήτου , a, b , c , ... τους γνωστούς και με τα μικρά αλλά τελευτία γράμματα της αλφαβήτου. .. x , y , z τους αγνώστους. Σε αυτήν την παράδοση χρωστάμε τον σημερινό συμβολισμό του αλφα χι τετράγωνο και βήτα χι και γάμα ίσον με μηδέν.
Σταχυολογήματα από το "Θεώρημα του παπαγάλου" (Βιβλίο του Ντένι Γκετζ)
1. Ο
Θαλής προσπάθησε να μετρήσει το ύψος των πυραμίδων της Αιγύπτου. Η
σκέψη του ήταν αρχικά ότι όταν η σκιά του γίνει ίση με το ύψος του τότε
και η σκιά της πυραμίδας θα ισούται με το ύψος της. Έστειλε έναν Αιγύπτιο στη βάση της πυραμίδας.Όταν υπολόγισε ότι η σκιά του έχει μήκος ίσο με το ύψος του ζήτησε από τον Αιγύπτιο να μετρήσει τη σκιά της πυραμίδας.
"Αφού δεν μπορώ να μετρήσω το ύψος που χάνεται στους ουρανούς θα μετρήσω τη σκιά που είναι πεσμένη στο έδαφος" , σκέφτηκε.
2. Ο Θαλής για πρώτη φορά στα μαθηματικά προσπάθησε να αποδείξει ισχυρισμούς που ισχύουν καθολικά , πάντα. Τον ενδιέφεραν ιδιότητες που ικανοποιούνται από μία απειρία αντικειμένων. Η πρώτη απόδειξη στην Ιστορία των μαθηματικών ήταν δική του και αφορούσε ότι η διάμετρος χωρίζει τον κύκλο σε δύο ίσα τόξα τα ημικύκλια. Κάθε διάμετρος κάθε κύκλου τον χωρίζει σε δύο ίσα μέρη. Αναζητούσε αποδείξεις που ισχύουν πάντοτε σε μιa απειρία αντικειμένων του ίδιου είδους.
" Δεν υπάρχει ούτε ένα τόσο δα μικρό , παράνομο και κρυμμένο κυκλάκι κάπου στον κόσμο που να έκανε αντάρτικο και να μην ικανοποιεί το θεώρημα του. Είναι τόσο σκληρό αυτό σχεδόν φασιστικό. Κι όμως τίποτα δεν μπορεί αν ξεφύγει από ένα θεώρημα ...!"
Στον ίδιο αποδίδονται κι άλλες αποδείξεις όπως ότι οι κατακορυφήν γωνίες είναι ίσες ή ότι οι προσκείμενες στη βάση γωνίες ισοσκελούς τριγώνου είναι ίσες. Αντίθετα η απόδειξη ότι το άθροισμα των γωνιών ενός τριγώνου ισούται με 180 μοίρες αποδίδεται ιστορικά στον Πυθαγόρα.
3. "Ισοσκελές τρίγωνο είναι αυτό που έχει δύο ίσες πλευρές. Δύο ίσα σκέλη, όπως λέει το όνομά του δηλαδή δύο ίσα πόδια.Έτσι σκαληνό τρίγωνο είναι αυτό που έχει άνισες πλευρές άρα τα σκέλη του δεν είναι ίσα.Το σκαλήνό τρίγωνο δεν έχει ίσο μήκος ποδιών όπως το ισοσκελές. Είναι λοιπόν ένα κουτσό τρίγωνο.Φανταστείτε μια άσκηση μαθηματικών που θα ξεκινούσε :
" Δίνεται ένα κουτσό τρίγωνο..." και θα αναφερόταν στο σκαληνό.
4. "Δεν υπάρχει εξίσωση χωρίς ισότητα. Ούτε δημοκρατία..."
5. "Οι αριθμοί στους αρχαίους Έλληνες διανοητές άρχιζαν από το δύο.Το μηδέν (ουδέν) έδειχνε ανυπαρξία , άρα δεν ήταν αριθμός. Το ένα φανέρωνε την ύπαρξη ενός αντικειμένου. Από το δύο και μετά μετρούνταν η ποσότητα δηλαδή άρχιζαν οι αριθμοί." Ο Αρχύτας ο Ταραντίνος ενέταξε για πρώτη φορά το ένα ως αριθμό ισότιμο με τους άλλους και θεώρησε ότι η αρίθμηση ξεκινά από το ένα.
6. Τα όμοια τρίγωνα έχουν τη ίδια μορφή αν και σε διαφορετικό μέγεθος(σμίκρυνση-μεγέθυνση). Χαρακτηριστική ιδιότητα των όμοιων σχημάτων είναι ότι έχουν ανάλογες πευρές.
"Η διατήρηση των αναλογιών σημαίνει διατήρηση της μορφής".
Όταν δηλαδή διατηρείται η αναλογία των πλευρών δύο σχημάτων τα σχήματα έχουν παρόμοια μορφή ( είναι δηλαδή όμοια) απλά σε διαφορετικό μέγεθος.
7. "Το μηδέν μετατρέπει την αρνητική απάντηση : ΔΕΝ ΕΧΕΙ ΤΙΠΟΤΑ στην θετική : ΕΧΕΙ ΜΗΔΕΝ. Την αρνητική απάντηση : ΔΕΝ ΕΙΝΑΙ στην θετικη : ΕΙΝΑΙ ΜΗΔΕΝ".
8. "Αν το μηδέν είναι το τίποτα , οι αρνητικοί αριθμοί είναι λιγότερο από το τίποτα."
9. "Το μηδέν είναι:
αδύναμο στην πρόσθεση
παντοδύναμο στον πολλαπλασιασμό
απαγορευμένο στη διαίρεση
εκκεντρικό στις δυνάμεις."
10. "Η πιθανότητα είναι παγιδευμένη ανάμεσα στο μηδέν και το ένα. Μοιάζει με μια κούπα καφέ με γάλα με διαφορετικές αναλογίες των δύο συστατικών του.. Ενα φλιτζάνι καφέ έχει μαύρο χρώμα και συμβολίζει το αδύνατο με πιθανότητα μηδέν.Ένα φλιτζάνι γάλα με άσπρο χρώμα είναι το βέβαιο με πιθανότητα ένα. Αναμιγνύοντας το καφέ με το γάλα φτιάχνουμε ένα μίγμα σε αποχρώσεις του καφέ. Αν βάλουμε λιγότερο γάλα έχουμε σκούρο χρώμα δηλαδή πιθανότητα κοντά στο μηδέν. Αν βάλουμε περισσότερο γάλα το χρώμα ανοίγει και πλησιάζει στο άσπρο δηλαδή η πιθανότητα πλησιάζει το ένα."
11. "Θηριοδαμαστής του αγνώστου σημαίνει αυτόν που καταπιάνεται να λύσει μια εξίσωση."
12. "Μιγαδικοί αρθμοί ονομάστηκαν γιατί είναι μιγάδες. Είναι δηλαδή απόγονοι ενός πραγματικού κι ενός φανταστικού αριθμού."
13. "Στα αραβικά κασρ σημαίνει σπασμένο και είναι ο αραβικός όρος για το κλάσμα. Από τότε πέρασε η παράδοση στη Δύση να επιλέγεται ο όρος σπασμένο στη κάθε γλώσσα για να αποδώσει την έννοια του κλάσματος. Άλλωστε και το 'κλάσμα' στα αρχαία σημαίνει κάτι που έσπασε σε κομμάτια.Θυμόμαστε την έκφαση του ευαγγελιστή που περιγράφει τον Μυστικό Δείπνο :' έκλασε ο Ιησούς τον άρτο...' , τον έσπασε δηλαδή σε κομμάτια και μοίρασε τα κλάσματα στους μαθητές"
14 Το σύμβολο = που δηλώνει την ισότητα ανακαλύφθηκε από τον Ρέκορντ στα 1557. Όταν τον ρώτησαν γιατί επέλεξε το συγκεκριμένο σύμβολο είπε ότι περιέχει δύο δίδυμες παράλληλες γραμμές. Τι πιο πανομοιότυπο (ίσο) λοιπόν από δύο δίδυμα;"
15. Η αριθμητική είναι η επιστήμη των ακεραίων αριθμών , ενώ η άλγεβρα η επιστήμη των εξισώσεων.
16. Ο λογάριθμος του γινομένου ισούται με το άθροισμα των λογαρίθμων :
log(xy) = logx + logy. Θέλεις πολλαπλασιασμό; Σου κάνω πρόσθεση.Καθώς οι μηχανισμοί της πόσθεσης είναι απλούστεροι των αντίστοιχων του πολλαπλασιασμού , οι ωφέλειες είνaι σημαντικές. Ο λογάριθμος λειτουργεί ως αποπολλαπλασιαστής. Παρομοίως για να κάνεις διαίρεση αρκεί να κάνεις αφαίρεση : log(x/y) = logx - logy.
17. "Καμιά μαθηματική πρόταση δεν πρέπει να γίνεται δεκτή χωρίς απόδειξη. Αυτός είναι ο άγραφος νόμος που θέσπισαν για τον εαυτό τους οι Έλληνες μαθηματικοί.Πώς όμως αποδεικνύουμε μια πρόταση; Συμπεραίνοντάς την από κάποια άλλη που γνωρίζουμε ότι είναι αληθής. Φαύλος κύκλος! Οι μαθηματικοί είναι λοιπόν καταδικασμένοι να δαγκώνουν την ουρά τους;Πώς θα σπάσουμε αυτόν τον κύκλο; Απαιτείται μια σωστή θεμελίωση. Είναι το αντίτιμο μιας μηχανής που στη συνέχεια θα δουλεύει σωστά και θα παρέχει αλήθειες. Ύστερα από μια σωστή θεμελίωση ο μηχανισμός θα συνεχίσει να δουλεύει με τη δική του δυναμική. Επομένως δεν μπορούμε να βγούμε από τον φαύλο κύκλο, παρά μόνο αν αποδεχθούμε στην εκκίνηση μερικές αλήθειες χωρίς απόδειξη.Τις θεσπίζουμε a priori μια για πάντα. Με τον τρόπο αυτόδούλεψε ο Ευκλείδης. Πρώτα θέσπισε ορισμούς και αμέσως μετά έρχονατι τα αιτήματα και τα αξιώματα.Τα πρώτα θεσπίζουν a priori ότι ορισμένες κατασκευές είναι δυνατές.Τα δεύτερα είναι κοινές έννοιες , δεκτές από όλους , αρχές της σκέψης που κανένας δεν αισθάνεται την ανάγκη να αμφισβητήσει την εγκυρότητά τους".
Μόσχος Αλέξανδρος
Κάνοντας κλικ παρακάτω θα δείτε μια εργασία μου με θέμα την διδακτική αξιοποίηση της Ιστορίας των μαθηματικών στην καθημερινή μάχιμη διδασκαλία.
Κλικ εδώ για την εργασία.
Bιογραφίες αρχαίων Ελλήνων μαθηματικών μπορείτε να βρείτε εδώ από video της Εκπαιδευτικής Τηλεόρασης της ΕΡΤ.
ΘΕΜΑΤΙΚΟΣ ΚΑΤΑΛΟΓΟΣ
Εδώ μπορείτε να βρείτε τα εξής θέματα Ιστορίας των μαθηματικών με την παρακάτω σειρά :
1. Η εξέλιξη των αριθμών
2. Η εμφάνιση της μεταβλητής
3. Το μηδέν και η άγνοια
4. Οι αρνητικοί αριθμοί
5. Η ιστορία του π
6. Ο αριθμός i - H απαρχή των μιγαδικών αριθμών.
7 . Η ιστορία των εξισώσεων ( σύνδεση με ιστοσελίδα)
8. Ιστορία του λογαρίθμου
9 Ο ασύλληπτος e
10. Ελληνικά μαθηματικά
11 Κωνσταντίνος Καραθεωδορής
12. Θαλής ο Μιλήσιος
13 Στοιχεία του Ευκλείδη
14 Πειραματική γεωμετρία (σύνδεση με ιστοσελίδα)
15 Μη ευκλείδειες γεωμετρίες ( σύνδεση με ιστοσελίδα )
16 Τα 3 άλυτα προβλήματα της ελληνικής αρχαιότητας
17. Ιστορικά προβλήματα γεωμετρίας του Θαλή Μιλήσιου.
( σύνδεση με ιστοσελίδα )
18. Ιστορία του πυθαγωρείου θεωρήματος ( σύνδεση με ιστοσελίδα )
19. Συνοπτική ιστορία της τριγωνομετρίας.
20. Συνοπτική ιστορία των αρχαιοελληνικών μαθηματικών.
21. Πίνακας ανάπτυξης των μαθηματικών.
22. Η ανθρωπολογία των μαθηματικών.
Αλφαβητικός κατάλογος κυριότερων μαθηματικών.
1. Η ΕΞΕΛΙΞΗ ΤΩΝ ΑΡΙΘΜΩΝ
Από την μελέτη της ιστορίας των μαθηματικών μπορούμε να διαπιστώσουμε ότι οι αρνητικοί αριθμοί παρά τη γνώση τους δεν νομιμοποιήθηκαν πριν περάσουν αρκετοί αιώνες! Οι αρχαίοι Αιγύπτιοι δεν αναφέρουν τους αρνητικούς αριθμούς. Αντίθετα, οι Έλληνες τους γνώριζαν, με κύριο εκφραστή το Διόφαντο. Τα ελληνικά γεωμετρικά θεωρήματα περιέχουν κανόνες για αρνητικά μεγέθη. Ο Βραχμαγκούπτα αναφέρει τους κανόνες των προσήμων. Όμως οι αρνητικοί αριθμοί δεν "νομιμοποιήθηκαν" αφού δεν θεωρούνταν λύσεις εξισώσεων. Οι Κινέζοι επίσης, δεν αντιμετώπιζαν προβλήματα στους υπολογισμούς θετικών και αρνητικών αφού χρησιμοποιούσαν τον άβακα με δύο ομάδες ράβδων (κόκκινες για τους θετικούς και μαύρες για τους αρνητικούς) (Boyer & Merzbach, 1997).
Η πρώτη εισαγωγή των σημερινών συμβόλων έγινε μόλις το 1489 και στην αρχή χρησιμοποιήθηκαν για να χρεώσουν πλεόνασμα ή έλλειψη των αποθηκών. Η πρώτη συστηματική προσπάθεια εμπέδωσης και μελέτης χρεώνεται στον Cardano Conjectandi στο έργο του Ars. Magna, η δε οριστική τους θεμελίωση επιτεύχθηκε στο 19ο αιώνα με τις συνολοθεωρητικές -αλγεβρικές μεθόδους που γνωρίζουμε (Boyer & Merzbach, 1997
Όταν οι αρχαίοι Βαβυλώνιοι άρχισαν να χτίζουν την πόλη - λέει ο θρύλος- ασχολήθηκαν ιδιαίτερα με τη γεωμετρία. Ήδη από τον 20ό αι. π.Χ. διαπίστωσαν ότι όταν η περιφέρεια οποιουδήποτε κύκλου διαιρείται δια της διαμέτρου του, και το αποτέλεσμα είναι πάντοτε περίπου τρία. Υπολόγισαν μάλιστα την τιμή αυτού του λόγου στα 25/8, τα οποία απέχουν μόλις κατά 0,5% της πραγματικής τιμής του. Πολύ λιγότερο ακριβής είναι η άλλη από τις αρχαιότερες τιμές του η, που συναντάμε στη Βίβλο (Βασιλέων Α, 7, 23), σύμφωνα με την οποία η κυκλική λίμνη του οίκου του Σολομώντα είχε διάμετρο δέκα πήχεις και περιφέρεια τριάντα πήχεις, τοποθετώντας την τιμή ακριβώς στο τρία.
Μία από τις αρχαιότερες και ακριβέστερες τιμές είναι αυτή του αιγυπτίου γραφέα Αχμές. Την έχει καταγράψει σε έναν πάπυρο του Μέσου Βασιλείου, περίπου το 1650 π.Χ., αντιγράφοντας ουσιαστικά έναν ακόμη αρχαιότερο πάπυρο. Ο Αχμές περιέγραψε το π ως το αποτέλεσμα της διαίρεσης του 256 διά του 81, δηλαδή 3,160.
Εκείνος όμως ο οποίος θεωρείται ότι ήταν ο πρώτος που προσέγγισε τον υπολογισμό π σε μια πιο θεωρητική βάση ήταν ο Αρχιμήδης, γι' αυτό και το π είναι γνωστό και ως σταθερά του Αρχιμήδη. Κινέζοι, Ινδοί και Πέρσες σοφοί προσπάθησαν όλοι να υπολογίσουν τη σταθερά αυτή. Ωστόσο, το όνομα με το οποίο τη γνωρίζουμε σήμερα της δόθηκε το 1706, όταν ο ουαλλός μαθηματικός Γουίλιαμ Τζόουνς πρότεινε να ονομαστεί η σταθερά του Αρχιμήδη με το ελληνικό γράμμα π, από τη λέξη "περιφέρεια".
Ωστόσο, οι μεγάλες δυσκολίες με το π τότε δεν είχαν ακόμη αρχίσει. Το 1761 ο Γιόχαν Λάμπερτ απέδειξε ότι το π είναι άρρητος αριθμός. Με απλά λόγια αυτό σημαίνει ότι δεν μπορεί να εκφραστεί ως κλάσμα δύο ακέραιων αριθμών. Στο σχολείο τα παιδιά μαθαίνουν ότι το π είναι περίπου 22/7, η τιμή αυτή είναι όμως και πάλι κατά προσέγγιση, γιατί το π βρίσκεται εκτός μαθηματικής λογικής.
Η δεύτερη μεγάλη ανακάλυψη σημειώθηκε το 1882, όταν ο Φέρντιναντ φον Λίντεμαν απέδειξε ότι το π είχε μία ακόμη ασυνήθιστη ιδιότητα: ήταν υπερβατικός αριθμός. Στη μαθηματική ορολογία αυτό σημαίνει ότι δεν αποτελεί τη ρίζα καμιάς αλγεβρικής εξίσωσης με ρητούς συντελεστές.
Στη μη μαθηματική ορολογία αυτό σημαίνει ότι το π αποτελεί την απόδειξη του παλαιού ρητού ότι δεν μπορεί κανείς να τετραγωνίσει τον κύκλο. Δεν μπορεί δηλαδή κανείς, χρησιμοποιώντας μόνο έναν κανόνα και έναν διαβήτη, να φτιάξει ένα τετράγωνο που να έχει ακριβώς το ίδιο εμβαδόν με έναν δεδομένο κύκλο.
Η κομψότητα της φύσης του π συνοψίζεται όμως στις τόσες προσπάθειες που έχουν γίνει και εξακολουθούν να γίνονται για τη συμπλήρωση των αριθμών του. Η επίμονη αναζήτηση ξεκίνησε ίσως με τον γερμανό μαθηματικό Λούντολφ βαν Τσόιλεν, ο οποίος γύρω στο 1600 υπολόγισε τα πρώτα 35 δεκαδικά ψηφία του π. Ηταν τόσο υπερήφανος γι᾿ αυτό το έργο, στο οποίο αφιέρωσε μεγάλο μέρος της ζωής του, που ζήτησε να γράψουν τα 35 ψηφία στην επιτύμβια στήλη του. Εξίσου επίμονος, ο Γουίλιαμ Σανκς αφιέρωσε από την πλευρά του 20 χρόνια στους υπολογισμούς προχωρώντας το π στα 707 δεκαδικά ψηφία. Δυστυχώς το επίτευγμα του υπέστη τεράστιο πλήγμα όταν οι πρώτο ψηφιακοί υπολογιστές ανακάλυψαν ότι είχε κάνει λάθος στο 528ο δεκαδικό ψηφίο, αχρηστεύοντας όλα τα επόμενα.
Η επέκταση του π στο άπειρο έχει επίσης επανειλημμένως προσελκύσει το ενδιαφέρον των συγγραφέων επιστημονικής φαντασίας. Ο σπουδαίος αμερικανός αστρονόμος Καρλ Σαγκάν στο βιβλίο του "Επαφή" έκρυψε την υπογραφή των εξωγήινων μέσα στα δήθεν τυχαία ψηφία του π, τα οποία στην πραγματικότητα δεν ακολουθούν κάποια συγκεκριμένη διάταξη.
"Ηταν πολύ πονηρό, γιατί αυτό δεν γίνεται" λέει ο καθηγητής Στιούαρτ. "Δεν μπορείς να τακτοποιήσεις το π σε συγκεκριμένη ακολουθία. Ήταν ένα ωραίο απατηλό τέχνασμα εκ μέρους του Σαγκάν. Υπό μίαν έννοιαν ούτε ο ίδιος ο Θεός δεν θα μπορούσε να βρει μια ακολουθία μέσα στο π", πρσοθέτει.
" Ένας νάνος στο ψηλότερο σκαλί είναι πιο ψηλά από ένα γίγαντα στο χαμηλότερο". Τι σχέση μπορεί να έχει η παραπάνω φράση με τα μαθηματικά; Έστω ο αριθμός 149. Το ψηφίο 1 είναι νάνος σχετικά με τον μεγαλύτερό του τον γίγαντα 9. Κι όμως το ένα είναι ψηλότερα , έχει μεγαλύτερη αξία από το 9 στον προηγούμενο αριθμό. Αυτό συμβαίνει γιατί βρίσκεται σε ψηλότερο σκαλί ( στο σκαλί των εκατοντάδων) από το χαμηλότερο που βρίσκεται το 9 (στο σκαλί των μονάδων). Η φράση αυτή λοιπόν αναφέρεται στο θεσιακό σύστημα αρίθμησης. Οι Ευρωπαίοι έμποροι βρήκαν αυτό το αριθμητικό σύστημα στους Άραβες και εντυπωσιάστηκαν. Το μετέφεραν αμέσως στη Δύση και από τοτε επικράτησε παγκοσμίως.Σήμεμα το αποκαλούμε αραβικό σύστημα αρίθμησης. Το σωστότερο βέβαια θα ήταν να το αποκαλούσαμε ινδοαραβικό. Κι αυτό γιατί λησμονούμε ότι οι Άραβες το δανείστηκαν από τους Ινδούς. Οι Ινδοί λοιπόν ανακάλυψαν και πρωτοχρησιμοποίησαν το θεσιακό σύστημα αρίθμησης. Ας σκεφτούμε τώρα τι σημαίνει η φράση : " Η αξία εξαρτάται από τη θέση". Τι σημαίνει άραγε για την αξία ενός ανθρώπου στην κοινωνία αλλά και για την αξία ενός ψηφίου ανάλογα με τη θέση του σε ένα αριθμό;
" Τον προσδιορισμό της θέσης ενός σημείου με τη χρήση συντεταγμένων την οφείλουμε στον Ντεκάρτ ( Καρτέσιο). Λέγεται ότι βρισκόταν ξαπλωμένος στο κρεβάτι του και παρατηρούσε μια μίγα που πετούσε διαρκώς πάνω από το κεφάλι του. Του γεννήθηκε ο προβληματισμός να προσδιορίσει την θέση της , μια και άλλαζε συνέχεια. Διαπίστωσε ότι του χρειαζόταν τρεις αριθμοί. Ένας για την απόσταση της από το ταβάνι και δύο ακόμη για τις αποστάσεις της από δύο πλαϊνούς τοίχους. Επρόκειτο για την πρώτη σύλληψη των τριών συνταταγμένων σημείου του χώρου".
" H πιο αιμοβαμμένη θεωρία στα μαθηματικά είναι σίγουρα η θεωρία ομάδων του Galois. Μονομάχησε με δύο φίλους της αγαπημένης του Stephanie. Η μονομαχία κατέληξε με το θάνατό του στα 21 του χρόνια. Σε γράμμα που απέστειλε νωρίτερα στον φίλο του Auguste Chevalier ο οποίος είχε στην κατοχή του χειρόγραφα της εργασίας του έγραφε :
«Αγαπημένοι μου φίλοι!
Προκλήθηκα από δύο πατριώτες – ήταν αδύνατον να αρνηθώ την πρόκληση. Σας ζητώ συγνώμη που δεν πήρα τη γνώμη κανενός σας. Οι αντίπaλοί μου, όμως μου ζήτησαν να δώσω το λόγο της τιμής μου ότι δεν θα ειδοποιήσω κανένα πατριώτη... Πεθαίνω, παντοτινά φίλος σας...
Προκλήθηκα από δύο πατριώτες – ήταν αδύνατον να αρνηθώ την πρόκληση. Σας ζητώ συγνώμη που δεν πήρα τη γνώμη κανενός σας. Οι αντίπaλοί μου, όμως μου ζήτησαν να δώσω το λόγο της τιμής μου ότι δεν θα ειδοποιήσω κανένα πατριώτη... Πεθαίνω, παντοτινά φίλος σας...
.... Εσύ Auguste Chevalier να ζητήσεις δημόσια από τον Jacobi ή τον Gauss να εκφέρουν τη γνώμη τους όχι πάνω στην ορθότητα, αλλά στη σημασία των θεωρημάτων. Ύστερα απ’αυτό, θα υπάρξουν ελπίζω μερικοί που θα θεωρήσουν ωφέλιμο γι’αυτούς να αποκρυπτογραφήσουν ό,τι περιέχεται σ’όλον αυτόν τον συρφετό».
Αυτός ο «συρφετός» δεν περιείχε τίποτα λιγότερο από τη θεωρία ομάδων, το κλειδί της σύγχρονης άλγεβρας και της σύγχρονης γεωμετρίας.
Μετά από λίγες μέρες από το θάνατο του Galois , ο φίλος παρουσίaσε την εργασία του στην Γαλλική Ακαδημία Επιστημών. Αμέσως αναγνωρίστηκε η σημασία της και σήμερα διδάσκεται σε όλα τα μαθηματικά τμήματα πανεπιστημίων διεθνώς. Είναι η περιβόητη Θεωρία ομάδων του Galois ".
Ο Galois λέγεται ότι είχε μεγάλη έφεση στα μαθηματικά. Ένας δάσκαλός του είπε γι' αυτόν ότι : "έχει την μανία των μαθηματικών" , κι ένας άλλος : " κυνηγάει την πρωτοτυπία". Η θεωρία των ομάδων έφερε μια επανάστaση στα μαθηματικά γιατί δεν επικεντρώνεται πλέον στους αριθμούς , ούτε στις συναρτήσεις αλλά στις δομές. Την εργασία του έφερε στο προσκήνιο άλλες δύο φορές. Την πρώτη όταν πρόεδρος της Γαλλικής Ακαδημίας ήταν ο Φουριέ. Δεν πρόλαβε όμως να τη φέρει στην ολομέλεια γιατί πέθανε ο Φουριέ και η εργασία έμεινε στα συρτάρια. Την δεύτερη φορά ο Galois έδωσε την εργασία στον διάδοχο του Φουριέ στον Πουανσόν. Εκείνος δεν κατάλaβε το πνεύμα της νέας εργασίας και έγραψε αρνητικά σχόλια. Δεν κατάλαβε το "καινούριο" που έφερνε η νέα θεωρία. Ο Galois πλήρωσε το ότι ήταν μπροστά από την εποχή του. Η εργασία του αναγνωρίστηκε μετά θάνατον μόλις την έφερε στην Ακαδημία ο φίλος του. Ο Galois έχει επίσης σημαντική συμμετοχή στην απόδειξη ότι οι εξισώσεις πέμπτου και άνω βαθμού δεν είναι επιλύσιμες με ριζικά. Θεωρείται ο βασιλιάς των μαθηματικών αντικειμένων που κυβερνούν την άλγεβρα του 20ου αιώνα. Εγκαινίασε τα λεγόμενα μοντέρνα μαθηματικά.
Μετά από λίγες μέρες από το θάνατο του Galois , ο φίλος παρουσίaσε την εργασία του στην Γαλλική Ακαδημία Επιστημών. Αμέσως αναγνωρίστηκε η σημασία της και σήμερα διδάσκεται σε όλα τα μαθηματικά τμήματα πανεπιστημίων διεθνώς. Είναι η περιβόητη Θεωρία ομάδων του Galois ".
Ο Galois λέγεται ότι είχε μεγάλη έφεση στα μαθηματικά. Ένας δάσκαλός του είπε γι' αυτόν ότι : "έχει την μανία των μαθηματικών" , κι ένας άλλος : " κυνηγάει την πρωτοτυπία". Η θεωρία των ομάδων έφερε μια επανάστaση στα μαθηματικά γιατί δεν επικεντρώνεται πλέον στους αριθμούς , ούτε στις συναρτήσεις αλλά στις δομές. Την εργασία του έφερε στο προσκήνιο άλλες δύο φορές. Την πρώτη όταν πρόεδρος της Γαλλικής Ακαδημίας ήταν ο Φουριέ. Δεν πρόλαβε όμως να τη φέρει στην ολομέλεια γιατί πέθανε ο Φουριέ και η εργασία έμεινε στα συρτάρια. Την δεύτερη φορά ο Galois έδωσε την εργασία στον διάδοχο του Φουριέ στον Πουανσόν. Εκείνος δεν κατάλaβε το πνεύμα της νέας εργασίας και έγραψε αρνητικά σχόλια. Δεν κατάλαβε το "καινούριο" που έφερνε η νέα θεωρία. Ο Galois πλήρωσε το ότι ήταν μπροστά από την εποχή του. Η εργασία του αναγνωρίστηκε μετά θάνατον μόλις την έφερε στην Ακαδημία ο φίλος του. Ο Galois έχει επίσης σημαντική συμμετοχή στην απόδειξη ότι οι εξισώσεις πέμπτου και άνω βαθμού δεν είναι επιλύσιμες με ριζικά. Θεωρείται ο βασιλιάς των μαθηματικών αντικειμένων που κυβερνούν την άλγεβρα του 20ου αιώνα. Εγκαινίασε τα λεγόμενα μοντέρνα μαθηματικά.
Tα τρία άλυτα προβλήματα της αρχαιότητας! Διπλασιασμός του κύβου , τριχοτόμηση γωνίας , τετραγωνισμός κύκλου. Όλα τα προβλήματα αυτά ξεκίνησαν ως γενίκευση κάποιων άλλων που είχαν επιλυθεί.
Τετραγωνισμός κύκλου. Να κατασκευαστεί δηλαδή με κανόνα και διαβήτη τετράγωνο που να να έχει εμβαδόν ίσο με δοθέντα κύκλο. Ο Ιπποκράτης ο Χίος κατάφερε να τετραγωνίσει μηνίσκους. Σε μια εποχή που ο τετραγωνισμός αφορούσε ευθύγραμμα σχήματα όπως ορθογώνια , παραλληλόγραμμα και τραπέζια , ο Ιπποκράτης τετραγώνισε καμπυλόγραμμο σχήμα. Γέννησε ξαφνικά τρελές ελπίδες για τον τετραγωνισμό του κύκλου. Αφού οι μηνίσκοι τετραγωνίζονται γιατί όχι και ο κύκλος;
Διπλασιασμός του κύβου. Να κατασκευαστεί με κανόνα και διαβήτη κύβος με διπλάσιο όγκο από ένα δοθέντα κύβο. Το πρόβλημα αυτό είναι γενίκευση του διπλασιασμού τετραγώνου : " Να κατασκευαστεί τετράγωνο με εμβαδόν διπλάσιο από ένα δοθέντα". Η λύση αυτού του προβλήματος είναι να κατασκευάσουμε τετράγωνο με πλευρά τη διαγώνιο του αρχικού τετραγώνου. Το νέο τετράγωνο έχει διπλάσιο εμβαδόν από το αρχικό.
Τριχοτόμηση γωνίας. Το πρόβλημα αυτό αποτελεί γενίκευση της τριχοτόμησης ευθύγραμμου τμήματος. Να χωριστεί δηλαδή ένα ευθύγραμμο τμήμα σε τρία ίσα μέρη. Η κατασκευή αυτή οφείλεται στον Θαλή με χρήση μιας βοηθητικής ημιευθείας και παράλληλων ευθειών. Επεκτάθηκε το πρόβλημα αυτό στην αναζήτηση δύο ημιευθειών που χωρίζουν μια γωνία σε τρία ίσα μέρη. Αφού το ευθύγραμμο τμήμα τριχοτομείται γιατί όχι και η γωνία;
Την εποχή εκείνη οι Έλληνες και οι Αιγύπτιοι πίστευαν ότι όλα τα προβλήματα έχουν λύση. Δεν μπορούσαν να φανταστούν ότι υπάρχουν προβλήματα άλυτα και ακόμη περισσότερο ότι μπορούμε να αποδείξουμε το αδύνατο της λύσης τους. Αργότερα λοιπόν αποδείχθηκε ότι η τριχοτόμηση μιας γωνίας , ο διπλασιασμός του κύβου και ο τετραγωνισμός του κύκλου με κανόνα διαβήτη ανήκουν στην κατηγορία των άλυτων προβλημάτων . Είναι άλυτα όχι γιατί εμείς δεν μπορούμε να τα επιλύσουμε όπως νόμιζαν οι αρχαίοι , αλλά γιατί αποδείχθηκε με σαφή τρόπο ότι είναι αδύνατο να λυθούν.
Το αδύνατο αυτών των κατασκευών στηρίχθηκε στην διαπίστωση ότι όλες αυτές οι γεωμετρικές κατασκευές συνδέονται με άρρητους αριθμούς που δεν είναι αλγεβρικοί αλλά υπερβατικοί. Αλγεβρικοί είναι εκείνοι οι άρρητοι που αποτελούν ρίζες μιας εξίσωσης με ακέραιους συντελεστές. Ο ρίζα 2 για παράδειγμα είναι αλγεβρικός γιατί είναι ρίζα της εξίσωσης: χ2 -2 =0. Ο π όμως είναι υπεβατικός γιατί δεν υπάρχει εξίσωση με ακέραιους συντελεστές που να έχει ρίζα το π. Ο τετραγωνισμός λοιπόν του κύκλου με κανόνα και διαβήτη είναι αδύνατος γιατί ο αριθμός π δεν είναι αλγεβρικός!
Οι πίνακες των χορδών από τον Ίππαρχο και τον Πτολεμαίο είναι τα πρώτα παραδείγματα συναρτήσεων στην ιστορία των μαθηματικών. Τριγωνομετρικών συναρτήσεων.Αργότερα οι Ινδοί αντικατέστησαν τους πίνακες χορδών με πίνακες ημιτόνων, που ήταν πιο εύχρηστοι.Το ημίτονο δεν είναι τίποτα άλλο από το μισό μιας χορδής ενός μοναδιαίου κύκλου. Η λέξη προέρχεται από το σανσκριτικό ζίβα που μεταφράζει την ελληνική έκφραση "χορδή τόξου" που χρησιμοποίησε ο Ίππαρχος. Στα αραβικά έγινε τζίμπα και στα λατινικά sinus. Ο πρώτος μαθηματικός που συνέταξε πίνακες ημιτόνων κι όχι χορδών ήταν ο Άραβας Αλ - Χουαρίσμι.Ο Αλ - Χασίμπ δημιούργησε τις εφαπτομένες. Ο Θαλής θα υπολόγιζε κατευθείαν το ύψος της πυραμίδας του Χέοπα αν διέθετε πίνακες εφαπτομένων. Δεν διέθετε όμως ... Γι' αυτό στηρίχθηκε στην θεωρία ομοιότητας.
Μια μέρα του 1742 ο μαθηματικός Κρίστιαν Γκόλντμπαχ έστειλε μια επιστολή στον Όιλερ , όπου έγραφε : "Κάθε άρτιος αριθμός διαφορετικός του 2 μπορεί να γραφεί ως άθροισμα δύο πρώτων αριθμών. Για παράδειγμα : 16 = 13 + 3 , 30 = 23 + 7". Πέρασαν δυόμισι αιώνες από τότε και εξακολουθούμε να μη γνωρίζουμε αν αυτή πρόταση , γνωστή ως εικασία του Γκόλντμπαχ , είναι αληθής.
Ένα σημείο Μ του επιπέδου με σαφή γεωμετρική υπόσταση μεταμορφώνεται με το μαγικό ραβδί των Φερμά και Ντεκάρτ σε ένα ζευγάρι αριθμών. Ακατα μακατα .... και το σημείο έγινε (x,y).Είναι μια πραγματική επανάσταση! Το γεωμετρικό σημείο πήρε αλγεβρική μορφή. Η καθαρή γεωμετρία έχει πια εξοβελιστεί. Το ίδιο συμβαίνει με τις γεωμετρικές καμπύλες. Η εξίσωσή τους γίνεται το αλγεβρικό τους όνομα!
Το σύμβολο"= " της ισότητας οφείλεται στον μαθηματικό και γιατρό Ρέκορντ στα 1557. Το "x" του πολλαπλασιασμού είναι επινόηση του Άγγλου Ουίλλιαμ Ούγκρεντ στα 1631.Τα σύμβολα "<" , ">" επινόηση του Άγγλου Τομας Χάρριοτ.Το σύμβολο της τετραγωνικής ρίζας από τον Γερμανό Ρούντολφ στα 1525. Το σύμβολο του απείρου από τον Άγγλο Τζον Ουάλλις. Ο συμβολισμός των δυνάμεων από τον Γάλλο Νικολά Συκέ τον 15ο αιώνα. Ο Ντεκάρτ τέλος συμβόλιζε με τα αρχικά μικρά γράμματα της αγγλικής αλφαβήτου , a, b , c , ... τους γνωστούς και με τα μικρά αλλά τελευτία γράμματα της αλφαβήτου. .. x , y , z τους αγνώστους. Σε αυτήν την παράδοση χρωστάμε τον σημερινό συμβολισμό του αλφα χι τετράγωνο και βήτα χι και γάμα ίσον με μηδέν.
Σταχυολογήματα από το "Θεώρημα του παπαγάλου" (Βιβλίο του Ντένι Γκετζ)
"Αφού δεν μπορώ να μετρήσω το ύψος που χάνεται στους ουρανούς θα μετρήσω τη σκιά που είναι πεσμένη στο έδαφος" , σκέφτηκε.
2. Ο Θαλής για πρώτη φορά στα μαθηματικά προσπάθησε να αποδείξει ισχυρισμούς που ισχύουν καθολικά , πάντα. Τον ενδιέφεραν ιδιότητες που ικανοποιούνται από μία απειρία αντικειμένων. Η πρώτη απόδειξη στην Ιστορία των μαθηματικών ήταν δική του και αφορούσε ότι η διάμετρος χωρίζει τον κύκλο σε δύο ίσα τόξα τα ημικύκλια. Κάθε διάμετρος κάθε κύκλου τον χωρίζει σε δύο ίσα μέρη. Αναζητούσε αποδείξεις που ισχύουν πάντοτε σε μιa απειρία αντικειμένων του ίδιου είδους.
" Δεν υπάρχει ούτε ένα τόσο δα μικρό , παράνομο και κρυμμένο κυκλάκι κάπου στον κόσμο που να έκανε αντάρτικο και να μην ικανοποιεί το θεώρημα του. Είναι τόσο σκληρό αυτό σχεδόν φασιστικό. Κι όμως τίποτα δεν μπορεί αν ξεφύγει από ένα θεώρημα ...!"
Στον ίδιο αποδίδονται κι άλλες αποδείξεις όπως ότι οι κατακορυφήν γωνίες είναι ίσες ή ότι οι προσκείμενες στη βάση γωνίες ισοσκελούς τριγώνου είναι ίσες. Αντίθετα η απόδειξη ότι το άθροισμα των γωνιών ενός τριγώνου ισούται με 180 μοίρες αποδίδεται ιστορικά στον Πυθαγόρα.
3. "Ισοσκελές τρίγωνο είναι αυτό που έχει δύο ίσες πλευρές. Δύο ίσα σκέλη, όπως λέει το όνομά του δηλαδή δύο ίσα πόδια.Έτσι σκαληνό τρίγωνο είναι αυτό που έχει άνισες πλευρές άρα τα σκέλη του δεν είναι ίσα.Το σκαλήνό τρίγωνο δεν έχει ίσο μήκος ποδιών όπως το ισοσκελές. Είναι λοιπόν ένα κουτσό τρίγωνο.Φανταστείτε μια άσκηση μαθηματικών που θα ξεκινούσε :
" Δίνεται ένα κουτσό τρίγωνο..." και θα αναφερόταν στο σκαληνό.
4. "Δεν υπάρχει εξίσωση χωρίς ισότητα. Ούτε δημοκρατία..."
5. "Οι αριθμοί στους αρχαίους Έλληνες διανοητές άρχιζαν από το δύο.Το μηδέν (ουδέν) έδειχνε ανυπαρξία , άρα δεν ήταν αριθμός. Το ένα φανέρωνε την ύπαρξη ενός αντικειμένου. Από το δύο και μετά μετρούνταν η ποσότητα δηλαδή άρχιζαν οι αριθμοί." Ο Αρχύτας ο Ταραντίνος ενέταξε για πρώτη φορά το ένα ως αριθμό ισότιμο με τους άλλους και θεώρησε ότι η αρίθμηση ξεκινά από το ένα.
6. Τα όμοια τρίγωνα έχουν τη ίδια μορφή αν και σε διαφορετικό μέγεθος(σμίκρυνση-μεγέθυνση). Χαρακτηριστική ιδιότητα των όμοιων σχημάτων είναι ότι έχουν ανάλογες πευρές.
"Η διατήρηση των αναλογιών σημαίνει διατήρηση της μορφής".
Όταν δηλαδή διατηρείται η αναλογία των πλευρών δύο σχημάτων τα σχήματα έχουν παρόμοια μορφή ( είναι δηλαδή όμοια) απλά σε διαφορετικό μέγεθος.
7. "Το μηδέν μετατρέπει την αρνητική απάντηση : ΔΕΝ ΕΧΕΙ ΤΙΠΟΤΑ στην θετική : ΕΧΕΙ ΜΗΔΕΝ. Την αρνητική απάντηση : ΔΕΝ ΕΙΝΑΙ στην θετικη : ΕΙΝΑΙ ΜΗΔΕΝ".
8. "Αν το μηδέν είναι το τίποτα , οι αρνητικοί αριθμοί είναι λιγότερο από το τίποτα."
9. "Το μηδέν είναι:
αδύναμο στην πρόσθεση
παντοδύναμο στον πολλαπλασιασμό
απαγορευμένο στη διαίρεση
εκκεντρικό στις δυνάμεις."
10. "Η πιθανότητα είναι παγιδευμένη ανάμεσα στο μηδέν και το ένα. Μοιάζει με μια κούπα καφέ με γάλα με διαφορετικές αναλογίες των δύο συστατικών του.. Ενα φλιτζάνι καφέ έχει μαύρο χρώμα και συμβολίζει το αδύνατο με πιθανότητα μηδέν.Ένα φλιτζάνι γάλα με άσπρο χρώμα είναι το βέβαιο με πιθανότητα ένα. Αναμιγνύοντας το καφέ με το γάλα φτιάχνουμε ένα μίγμα σε αποχρώσεις του καφέ. Αν βάλουμε λιγότερο γάλα έχουμε σκούρο χρώμα δηλαδή πιθανότητα κοντά στο μηδέν. Αν βάλουμε περισσότερο γάλα το χρώμα ανοίγει και πλησιάζει στο άσπρο δηλαδή η πιθανότητα πλησιάζει το ένα."
11. "Θηριοδαμαστής του αγνώστου σημαίνει αυτόν που καταπιάνεται να λύσει μια εξίσωση."
12. "Μιγαδικοί αρθμοί ονομάστηκαν γιατί είναι μιγάδες. Είναι δηλαδή απόγονοι ενός πραγματικού κι ενός φανταστικού αριθμού."
13. "Στα αραβικά κασρ σημαίνει σπασμένο και είναι ο αραβικός όρος για το κλάσμα. Από τότε πέρασε η παράδοση στη Δύση να επιλέγεται ο όρος σπασμένο στη κάθε γλώσσα για να αποδώσει την έννοια του κλάσματος. Άλλωστε και το 'κλάσμα' στα αρχαία σημαίνει κάτι που έσπασε σε κομμάτια.Θυμόμαστε την έκφαση του ευαγγελιστή που περιγράφει τον Μυστικό Δείπνο :' έκλασε ο Ιησούς τον άρτο...' , τον έσπασε δηλαδή σε κομμάτια και μοίρασε τα κλάσματα στους μαθητές"
14 Το σύμβολο = που δηλώνει την ισότητα ανακαλύφθηκε από τον Ρέκορντ στα 1557. Όταν τον ρώτησαν γιατί επέλεξε το συγκεκριμένο σύμβολο είπε ότι περιέχει δύο δίδυμες παράλληλες γραμμές. Τι πιο πανομοιότυπο (ίσο) λοιπόν από δύο δίδυμα;"
15. Η αριθμητική είναι η επιστήμη των ακεραίων αριθμών , ενώ η άλγεβρα η επιστήμη των εξισώσεων.
16. Ο λογάριθμος του γινομένου ισούται με το άθροισμα των λογαρίθμων :
log(xy) = logx + logy. Θέλεις πολλαπλασιασμό; Σου κάνω πρόσθεση.Καθώς οι μηχανισμοί της πόσθεσης είναι απλούστεροι των αντίστοιχων του πολλαπλασιασμού , οι ωφέλειες είνaι σημαντικές. Ο λογάριθμος λειτουργεί ως αποπολλαπλασιαστής. Παρομοίως για να κάνεις διαίρεση αρκεί να κάνεις αφαίρεση : log(x/y) = logx - logy.
17. "Καμιά μαθηματική πρόταση δεν πρέπει να γίνεται δεκτή χωρίς απόδειξη. Αυτός είναι ο άγραφος νόμος που θέσπισαν για τον εαυτό τους οι Έλληνες μαθηματικοί.Πώς όμως αποδεικνύουμε μια πρόταση; Συμπεραίνοντάς την από κάποια άλλη που γνωρίζουμε ότι είναι αληθής. Φαύλος κύκλος! Οι μαθηματικοί είναι λοιπόν καταδικασμένοι να δαγκώνουν την ουρά τους;Πώς θα σπάσουμε αυτόν τον κύκλο; Απαιτείται μια σωστή θεμελίωση. Είναι το αντίτιμο μιας μηχανής που στη συνέχεια θα δουλεύει σωστά και θα παρέχει αλήθειες. Ύστερα από μια σωστή θεμελίωση ο μηχανισμός θα συνεχίσει να δουλεύει με τη δική του δυναμική. Επομένως δεν μπορούμε να βγούμε από τον φαύλο κύκλο, παρά μόνο αν αποδεχθούμε στην εκκίνηση μερικές αλήθειες χωρίς απόδειξη.Τις θεσπίζουμε a priori μια για πάντα. Με τον τρόπο αυτόδούλεψε ο Ευκλείδης. Πρώτα θέσπισε ορισμούς και αμέσως μετά έρχονατι τα αιτήματα και τα αξιώματα.Τα πρώτα θεσπίζουν a priori ότι ορισμένες κατασκευές είναι δυνατές.Τα δεύτερα είναι κοινές έννοιες , δεκτές από όλους , αρχές της σκέψης που κανένας δεν αισθάνεται την ανάγκη να αμφισβητήσει την εγκυρότητά τους".
Η γνώμη μου
Ιστορία μαθηματικών και η Διδακτική αξιοποίησή της
Έχει γίνει πολύ συζήτηση για την διδακτική αξιοποίηση της Ιστορίας των Μαθηματικών. Της έχουν αναγνωρίσει πολλά πλεονεκτήματα όπως ο εξανθρωπισμός της μαθηματικής παιδείας , η ανάδειξη του κοινωνικού χαρακτήρα των μαθηματικών , η ελκυστικότητα της κ.α
Είναι σίγουρα θετικό που στο τέλος των κεφαλαίων ή ενδιάμεσα στο τέλος μιας παραγράφου υπάρχουν ιστορικά σημειώματα.
Κατά την άποψη μου όμως η μετοχή της Ιστορίας θα μπορούσε να είναι πιο ουσιαστική παρά διακοσμητική. Αυτό θα γινόταν αν στην αρχή κάθε κεφαλαίου ή και παραγράφου αν ήταν δυνατόν θα υπήρχε ιστορική επισκόπηση τη ς νέας έννοιας.
Με τον τρόπο αυτό οι μαθητές πρέπει να δουν για ποιους λόγους και ποιες ανάγκες ξεκίνησε η εισαγωγή της νέας έννοιας. Ποια προβλήματα ήρθε να λύσει και σε ποια εποχή. Επίσης από ποια εξελικτικά στάδια πέρασε μέχρι την σημερινή της μορφή. Τέλος ποιοι μαθηματικοί συνέβαλαν στην θεμελίωσή της . Προωθείται έτσι η κοινωνική διάσταση των μαθηματικών , η σχέση τους με τα πραγματικά προβλήματα καθώς και η επίπονη εξελικτική τους πορεία.
Συνήθως διδάσκουμε τις έννοιες φορμαλιστικά ξεκομένα από το κοινωνικό γίγνεσθαι που τις γέννησε .Επίσης πάντα με την τελική τους μορφή που έχει όμως στην πλάτη της μια πορεία αλλαγών πολλών αιώνων. Παρατηρείται αυτό που η διδακτική φαινομενολογία οναμάζει αντιδιδακτική αντιστροφή. Προηγείται δηλαδή το αποτέλεσμα της αιτίας και της πορείας.
Πράδειγμα 1 : Ολοκληρώματα
Ξεκινούμε την διδασκαλία του ολοκληρώματος με τον αυστηρό ορισμό του αόριστου από τον Riemann. Προϊόν δηλαδή του 19ου αιώνα όπου κυριαρχούσε ο φορμαλισμός και η αναζήτηση των τυποκρατικών θεμελίων των μαθηματικών. Το ολοκήρωμα όμως δεν ξεκίνησε έτσι. Πρέπει να δούμε την προσπάθεια του Αρχιμήδη από την αρχαιότητα κιόλας να υπολογίσει τα εμβαδά παραβολικών χωρίων. Κατόπιν τον 17ο - 18 αιώνα που στην προσπάθεια να υπολογιστούν εμβαδά αναπτύχθηκαν οι πρώτοι κανόνες ορισμένου ολοκληρώματος με σημαντικό πρωτεργάτη τον Euler. Και τέλος να φτάσουμε στον 19ο αιώνα , αιώνα της θεωρίας και της φιλοσοφίας όπου ορίζεται πέον αυστηρά. Ο Riemann όμως γνώριζε την ιστορική πορεία του ολοκληρώματος όταν το όριζε αυστηρά , οι μαθητές πως όχι;
Παράδειγμα 2 : Τριγωνομετρία
Δεν μπορούμε να διδάσκουμε τριγωνομετρία χωρίς τα ιστορικά προβλήματα της μέτρησης του ύψους πανύψηλου δέντρου ή ψηλού γενικά αντικειμένου. Απλούστατα γιατί από εκεί ξεκίνησε . Αυτή είναι η αιτία που την γέννησε.
Παράδειγμα 3 : Όμοια τρίγωνα
Δεν μπορούμε να διδάσκουμε όμοια τρίγωνα χωρίς τα ιστορικά προβλήματα του Θαλή όπως :
Μέτρηση ύψους πυραμίδας
Μέτρηση ύψους δέντρου με το ραβδί και τη σκιά.
Μέτρηση της απόστασης πλοίου από την ακτή.
Κάνοντας κλικ παρακάτω θα δείτε μια εργασία μου με θέμα την διδακτική αξιοποίηση της Ιστορίας των μαθηματικών στην καθημερινή μάχιμη διδασκαλία.
Κλικ εδώ για την εργασία.
Παρακάτω θα βρείτε σε μορφή Power Point ιστορικά στοιχεία σε διάφορα μαθηματικά πεδία γνώσης.
Ιστορική παρουσίαση μαγικών τετραγώνων
Ιστορία των αρνητικών αριθμών
Ιστορική παρουσίαση τετραγωνικών ριζών
Στοιχεία του Ευκλείδη
Ιστορικά προβλήματα στην επίλυση εξισώσεων
Ιστορία των άρρητων αριθμών
Ιστορική παρουσίαση τετραγωνικών ριζών
Στοιχεία του Ευκλείδη
Ιστορικά προβλήματα στην επίλυση εξισώσεων
Ιστορία των άρρητων αριθμών
Bιογραφίες αρχαίων Ελλήνων μαθηματικών μπορείτε να βρείτε εδώ από video της Εκπαιδευτικής Τηλεόρασης της ΕΡΤ.
ΘΕΜΑΤΙΚΟΣ ΚΑΤΑΛΟΓΟΣ
Εδώ μπορείτε να βρείτε τα εξής θέματα Ιστορίας των μαθηματικών με την παρακάτω σειρά :
1. Η εξέλιξη των αριθμών
2. Η εμφάνιση της μεταβλητής
3. Το μηδέν και η άγνοια
4. Οι αρνητικοί αριθμοί
5. Η ιστορία του π
6. Ο αριθμός i - H απαρχή των μιγαδικών αριθμών.
7 . Η ιστορία των εξισώσεων ( σύνδεση με ιστοσελίδα)
8. Ιστορία του λογαρίθμου
9 Ο ασύλληπτος e
10. Ελληνικά μαθηματικά
11 Κωνσταντίνος Καραθεωδορής
12. Θαλής ο Μιλήσιος
13 Στοιχεία του Ευκλείδη
14 Πειραματική γεωμετρία (σύνδεση με ιστοσελίδα)
15 Μη ευκλείδειες γεωμετρίες ( σύνδεση με ιστοσελίδα )
16 Τα 3 άλυτα προβλήματα της ελληνικής αρχαιότητας
17. Ιστορικά προβλήματα γεωμετρίας του Θαλή Μιλήσιου.
( σύνδεση με ιστοσελίδα )
18. Ιστορία του πυθαγωρείου θεωρήματος ( σύνδεση με ιστοσελίδα )
19. Συνοπτική ιστορία της τριγωνομετρίας.
20. Συνοπτική ιστορία των αρχαιοελληνικών μαθηματικών.
21. Πίνακας ανάπτυξης των μαθηματικών.
22. Η ανθρωπολογία των μαθηματικών.
Αλφαβητικός κατάλογος κυριότερων μαθηματικών.
1. Η ΕΞΕΛΙΞΗ ΤΩΝ ΑΡΙΘΜΩΝ
Ο άνθρωπος χρειάστηκε 1.000.000 χρόνια για να οδηγηθεί στην αφηρημένη έννοια των αριθμών.
4. Οι αρνητικοί αριθμοί
Ο Homo sapiens (300.000 χρόνια πριν) κάνει μια μικρή αρίθμηση με κλαδιά.
Ο Homo sapiens sapiens (100.000 χρόνια πριν) χρησιμοποιεί κάποιες αριθμητικές λέξεις.
Οι κυνηγοί-τροφοσυλλέκτες (70.000-20.000 χρόνια πριν) καταλάβαιναν την απλή πρόσθεση, τον πολλαπλασιασμό και την αφαίρεση. Το μοίρασμα της τροφής τους σημαίνει ότι κατανοούσαν τη διαίρεση.
Η παλαιότερη ένδειξη αριθμητικής καταγραφής βρέθηκε στη Σουαζιλάνδη της Νότιας Αφρικής και είναι μια περόνη μπαμπουίνου με 29 εμφανείς εγκοπές που χρονολογείται από το 35.000 π.Χ. Μοιάζει με τα «ημερολογιακά ραβδιά» που ακόμα χρησιμοποιούν στη Ναμίμπια για να καταγράφουν την παρέλευση του χρόνου. Άλλα κόκαλα, της νεολιθικής περιόδου, έχουν βρεθεί στη Δυτική Ευρώπη. Μια κερκίδα λύκου που βρέθηκε στην Τσεχία και χρονολογείται από το 30.000 π.Χ. φέρει 55 εγκοπές σε δύο σειρές ανά πέντε, οι οποίες μάλλον αποτελούν καταγραφή θηραμάτων.
Οι Σουμέριοι ζύγιζαν, υπολόγιζαν τη γη σε «σαρ», μετρούσαν τα υγρά σε «κα», χρησιμοποιούσαν κλάσματα και είχαν σύστημα αριθμών με βάση το 60. π.Χ.
Το αριθμητικό τους σύστημα είχε ως βάση το 60 , ήταν μη ψηφιακό, θεσιακό, χωρίς υποδιαστολή και χωρίς μηδέν. Υποστηρίζεται ότι γνωρίζανε και το δεκαδικό σύστημα.
υπολογισμό των πρώτων αριθμών.
Το τρίγωνο του Pascal.
2. Η ΕΜΦΑΝΙΣΗ ΓΙΑ ΠΡΩΤΗ ΦΟΡΑ ΤHΣ ΜΕΤΑΒΛΗΤΗΣ
Το εξηνταδικό σύστημα των Βαβυλωνίων έχει επιβιώσει μέχρι σήμερα στο μέτρημα του χρόνου. Έτσι π.Χ. όταν οι Βαβυλώνιοι ήθελαν να εκφράσουν τον αριθμό 75, έλεγαν «1,15», όπως κι εμείς σήμερα τα 75 λεπτά τα εκφράζουμε σαν 1 ώρα και 15 λεπτά. π.Χ. Οι Αιγύπτιοι χρησιμοποιούν σύστημα αριθμών με βάση το 10.
Στο βαβυλωνιακό, το αιγυπτιακό, το ρωμαϊκό και πολλά άλλα αριθμητικά συστήματα της αρχαιότητας το τρία παριστάνεται ως ΙΙΙ. , επειδή κάθε φορά που συμπληρώνονται δέκα μονάδες δημιουργείται μια μονάδα ανωτέρας τάξης. Οι αριθμοί από το 0 μέχρι το 9 είναι μονοψήφιοι. Ο αριθμός 10 γράφεται ως ένα και μηδέν δηλαδή μια μονάδα ανωτέρας τάξης (δεκάδα) και καμιά απλή μονάδα. , γιατί η αξία του κάθε ψηφίου καθορίζεται από τη θέση του μέσα στον αριθμό. Έτσι στο 4737 από δεξιά προς τα αριστερά η αξία αυξάνεται. (δέκατα, εκατοστά, χιλιοστά, …) τότε η υποδιαστολή μας δείχνει που σταματούν οι ακέραιες μονάδες και που αρχίζουν οι κλασματικές. 31,2 από το 3,12 είναι η υποδιαστολή. , αφού απαιτούνται 60 απλές μονάδες για να δημιουργήσουν μια μονάδα ανωτέρας τάξεως, μια εξηντάδα. Με εξήντα εξηντάδες (3.600 απλές μονάδες) φτιάχνουμε μια μονάδα ανωτέρας τάξεως, μια τρισχιλιοεξακοσάδα, κ.ο.κ Έτσι ο αριθμός 125 απαρτίζεται από δύο (δύο εξηντάδεις=120) και το πέντε (πέντε μονάδες), ενώ ο αριθμός 634 απαρτίζεται από το δέκα (δέκα εξηντάδες=600) και το 24 (24 μονάδες). μ.Χ.
2852π.Χ. Ο Κινέζικος πολιτισμός χρησιμοποιεί σύστημα αριθμών με βάση το 60. Κάνανε αστρονομικούς υπολογισμούς 1500 χρόνια πριν από τους αρχαίους Έλληνες. , αόριστες εξισώσεις, αρνητικούς αριθμούς.
Οι Ίνκας έφτιαξαν ένα αριθμητικό σύστημα με βάση το 10, για να παρακολουθούν τις καθημερινές δραστηριότητες του μεγάλου πληθυσμού τους (Μέσα σε 200 χρόνια είχαν πληθυσμό 6-12.000.000 άτομα).
Οι Μάγια είχαν αριθμητικό σύστημα εικοσαδικό, μη ψηφιακό, θεσμικό και με ειδικό σύμβολο για το μηδέν. Το εικοσαδικό σύστημα οφείλεται ενδεχομένως στη χρήση των δαχτύλων τόσο των χεριών όσο και των ποδιών, για τη στοιχειώδη μέτρηση.
Οι Ινδοί έχουν το δεκαδικό σύστημα αρίθμησης, το οποίο χρησιμοποιείται παγκοσμίως και το οποίο διέδωσαν οι Άραβες. Άραβες μαθηματικοί ήταν ο αλ Χβαρίσμι (780-850 μ.Χ.), πατέρας της Άλγεβρας, τίτλο που διεκδικεί από το δικό μας Διόφαντο και ο Πέρσης ποιητής και αστρονόμος Ομάρ Χαγιάμ (1048-1131 μ.Χ.) (1180-1250 μ.Χ.). Για να τα υιοθετήσουν όμως οι Ευρωπαίοι χρειάστηκαν ακόμα 400 χρόνια.
Τα επιτεύγματα των Ελλήνων, για 1000 χρόνια επισκιάζουν όλα τα πνευματικά επιτεύγματα των επόμενων 1500 ετών. Οι Έλληνες όμως στηρίχτηκαν στις παλαιότερες αρχαίες κοινωνίες των Βαβυλωνίων και Αιγυπτίων. 10: το Ηρωδιανό ή Αττικό και το Ιωνικό ή Αλεξανδρινό. Δε χρησιμοποιούσαν τιμές θέσεις όπως έκανα οι Βαβυλώνιοι και όπως γίνεται σήμερα. Επίσης δε χρησιμοποιούσαν το μηδέν και τα κλάσματα.
" Το κόσκινο του Ερατοσθένη" για τον Οι Ινδοί έχουν το δεκαδικό σύστημα αρίθμησης, το οποίο χρησιμοποιείται παγκοσμίως και το οποίο διέδωσαν οι Άραβες. Άραβες μαθηματικοί ήταν ο αλ Χβαρίσμι (780-850 μ.Χ.), πατέρας της Άλγεβρας, τίτλο που διεκδικεί από το δικό μας Διόφαντο και ο Πέρσης ποιητής και αστρονόμος Ομάρ Χαγιάμ (1048-1131 μ.Χ.) (1180-1250 μ.Χ.). Για να τα υιοθετήσουν όμως οι Ευρωπαίοι χρειάστηκαν ακόμα 400 χρόνια.
Τα επιτεύγματα των Ελλήνων, για 1000 χρόνια επισκιάζουν όλα τα πνευματικά επιτεύγματα των επόμενων 1500 ετών. Οι Έλληνες όμως στηρίχτηκαν στις παλαιότερες αρχαίες κοινωνίες των Βαβυλωνίων και Αιγυπτίων. 10: το Ηρωδιανό ή Αττικό και το Ιωνικό ή Αλεξανδρινό. Δε χρησιμοποιούσαν τιμές θέσεις όπως έκανα οι Βαβυλώνιοι και όπως γίνεται σήμερα. Επίσης δε χρησιμοποιούσαν το μηδέν και τα κλάσματα.
υπολογισμό των πρώτων αριθμών.
Το τρίγωνο του Pascal.
2. Η ΕΜΦΑΝΙΣΗ ΓΙΑ ΠΡΩΤΗ ΦΟΡΑ ΤHΣ ΜΕΤΑΒΛΗΤΗΣ
Για πρώτη φορά χρησιμοποιήθηκε γράμμα για να παραστήσει ζητούμενο αριθμό από τον Διόφαντο στα 250 π.Χ στο έργο του : " Αριθμητικά ". Διατύπωσε και έλυσε ένα πρόβλημα χρησιμοποίώντας το γράμμα ( ανάποδο ς ).
Γράφει :
" Τον επιταχθέντα αριθμόν διελείν εις δύο αριθμούς εν υπεροχή τη δοθείσει.Έστω δει ο ρ , η δε υπεροχή Μμ , ευρείν τους αριθμούς...".
Δηλ : Δοθέντος αριθμού να διαιρεθεί σε δυο άλλουςπου έχουν δοθείσα διαφορά. Έστω ότιο δοθείς αριθμός είναι ο 100 η δε διαφορά 40. Να βρεθούν οι δύο αριθμοί.
Και συνεχίζει :
" Τετάχθω ο ελάσσων ςα ο άρα μείζων έσται ς α Μμ συναμφότεροιάρα γίνονται ςβμμ δέδονται δε Μρ.Μ άρα ρ ίσαι εισιν ςβ Μμ".
Το γράμμα ς που ο διόφαντος για πρώτη φορά χρησιμοποιεί έχει τελείως διαφορετικό νόημα από τα άλλα γράμματα.Συμβολίζει τον ζητούμενο αριθμό.Έναν συγκεκριμένο αλλά άγνωστο αριθμό.Οι μ ,ρ ,β συμβολίζουν αριθμούς σύμφωνα με την αρχαιοελληνική γραφή αριθμών.
3. Tο μηδέν και η άγνοια
Ήταν ο μεγάλος φιλόσοφος Λούντβιχ Bιττγκενστάϊν που είχε γράψει πως τα όρια της γλώσσας είναι και τα όρια της γνώσης μας για τον κόσμο.
Tο ίδιο ισχύει και για την τελειότερη ίσως γλώσσα που εφηύρε ο άνθρωπος, τα μαθηματικά. Tα όρια της φαντασίας μας ήταν και τα όρια της γλώσσας μας. Γι' αυτό και στα αριθμητικά συστήματα των αρχαίων Eλλήνων (α, β, γ, δ, στ, ...) και των Λατίνων (I,II, III, IV...) δεν υπήρξε ποτέ το στοιχείο μηδέν. Για το κυρίαρχο ρεύμα της αρχαιοελληνικής φιλοσοφίας, που συνοψίστηκε από τον Aριστοτέλη το κενό δεν μπορούσε να υπάρξει – ή όπως θα μπορούσε να λεχθεί: η μη ύπαρξη απλώς δεν υπήρχε. H ύπαρξη της ανυπαρξίας ήταν μια τεράστια λογική αντίφαση. Αρα δεν υπήρχε και κανένας λόγος να απεικονιστεί... αυτό που δεν υπήρχε. Aντίθετα για τις ανατολικές φιλοσοφίες, που τράβηξαν άλλους δρόμους και η πλήρης ανυπαρξία ήταν ζητούμενο της ανθρώπινης ύπαρξης, το μηδέν υπήρχε και μπορούσε – ή καλύτερα, έπρεπε – να απεικονιστεί.Φαντάζει παράδοξο ίσως πως κοινωνίες ολόκληρες πορεύτηκαν χωρίς την έννοια του μηδενός, μαθηματικά συστήματα στήθηκαν χωρίς αυτό το μαγικό στρογγυλό σύμβολο.
Οι Βαβυλώνιοι ήταν οι πρώτοι που χρησιμοποίησαν τον μηδέν όχι όμως ως αριθμό αλλά ως δείκτη.
Οι Έλληνες παρά την πρωτοποριακή θεώρηση που έκαναν στα Μαθηματικά δεν είδαν τον μηδέν ούτε ως αριθμό ούτε ως σύμβολο δείκτη για τη θέση των άλλων. Οι αριθμοί που ήταν αναγκαίο να έχουν όνομα ήταν εκείνοι που χρησιμοποιούσαν οι έμποροι και όχι οι μαθηματικοί. Υπήρχαν όμως και εξαιρέσεις και οι εξαιρέσεις αυτές ήταν οι μαθηματικοί αστρονόμοι. Μπορεί ορισμένοι ιστορικοί να υποστήριξαν ότι οι Έλληνες χρησιμοποίησαν το γράμμα όμικρον – αρχικό της λέξης ΟΥΔΕΝ - ως σύμβολο του μηδενός αλλά ο Neugebauer απέρριψε την εικασία υποστηρίζοντας πλην των άλλων ότι οι Έλληνες χρησιμοποιούσαν το όμικρον ως τον αριθμό 70. Πάντως έναν αιώνα μετά Χριστόν, ο Κλαύδιος Πτολεμαίος χρησιμοποιεί το βαβυλωνιακό μηδέν ως δείκτη.
Η ιδέα του μηδενός δείκτη θα κάνει την επανεμφάνισή της στην Ινδία ενώ το έτος 500 ο Aryabhata θα παρουσιάσει ένα σύστημα καταγραφής των αριθμών που θυμίζει το σημερινό αλλά ο μηδέν ως αριθμός δεν υπάρχει.
ΤΟ ΜΗΔΕΝ ΕΡΧΕΤΑΙ ΣΤΗΝ ΕΥΡΩΠΗ. Το 12ο αιώνα μ.Χ. το μηδέν ήρθε και στην Ευρώπη, ύστερα από 600 χρόνια καθυστέρησης! Οι Άραβες, επηρεασμένοι από τους Ινδούς, υιοθέτησαν αμέσως το σύστημά τους και το διέδωσαν στους γύρω λαούς, προσθέτοντας μάλιστα σε αυτό το θαυμαστό λογισμό δικές τους ανακαλύψεις, ιδιαίτερα σημαντικές. Με την επέκτασή τους στην Ευρωπαϊκή ήπειρο, μετέφεραν και αυτές τις μεθόδους τους. Ο Σαμανίδης Μοχάμεντ Ίμπν Μουσσά αλ-Χοβαρεσμί (από το όνομα του οποίου προέκυψε ο όρος αλγόριθμος) έγραψε δύο δοκίμια τα οποία μεταφέρθηκαν στη Δύση. Όμως κάθε εχέφρων και ορθά σκεπτόμενος Ευρωπαίος που ήθελε να χρησιμοποιήσει ή να μεταδώσει την εκπληκτική αυτή γνώση, χρειαζόταν πολύ περισσότερα από αυτά τα δύο βιβλία. Έπρεπε να βρει έναν τρόπο να αντιμετωπίσει τον τρομακτικό συντηρητισμό της δυτικής θρησκείας που έστελνε στη πυρά όποιον τολμούσε να χρησιμοποιήσει τα σύμβολα των «απίστων», δηλαδή τους αριθμούς 1 έως 9. Τα εμπόδια που όρθωσε ο παραλογισμός του θρησκευτικού συντηρητισμού της Ευρώπης διατηρήθηκαν ως το τέλος του Μεσαίωνα και άρχισαν να αίρονται με τις σταυροφορίες από τις οποίες οι Δυτικοί κατακτητές γύρισαν επηρεασμένοι από την παιδεία των Αράβων. Λίγους αιώνες αργότερα, τα γαλλικά και τα γερμανικά πανεπιστήμια, στα οποία μέχρι τον 14ο και τον 15ο αιώνα μ.Χ. μόλις και μετά βίας διδάσκονταν πρόσθεση και αφαίρεση, την περίοδο 1804 - 1851 (Αναγέννηση) χρησιμοποιούσαν πλέον σταθερά το ινδικοαραβικό σύστημα αριθμητικής, που τελικά θριάμβευσε.
3. Tο μηδέν και η άγνοια
Ήταν ο μεγάλος φιλόσοφος Λούντβιχ Bιττγκενστάϊν που είχε γράψει πως τα όρια της γλώσσας είναι και τα όρια της γνώσης μας για τον κόσμο.
Tο ίδιο ισχύει και για την τελειότερη ίσως γλώσσα που εφηύρε ο άνθρωπος, τα μαθηματικά. Tα όρια της φαντασίας μας ήταν και τα όρια της γλώσσας μας. Γι' αυτό και στα αριθμητικά συστήματα των αρχαίων Eλλήνων (α, β, γ, δ, στ, ...) και των Λατίνων (I,II, III, IV...) δεν υπήρξε ποτέ το στοιχείο μηδέν. Για το κυρίαρχο ρεύμα της αρχαιοελληνικής φιλοσοφίας, που συνοψίστηκε από τον Aριστοτέλη το κενό δεν μπορούσε να υπάρξει – ή όπως θα μπορούσε να λεχθεί: η μη ύπαρξη απλώς δεν υπήρχε. H ύπαρξη της ανυπαρξίας ήταν μια τεράστια λογική αντίφαση. Αρα δεν υπήρχε και κανένας λόγος να απεικονιστεί... αυτό που δεν υπήρχε. Aντίθετα για τις ανατολικές φιλοσοφίες, που τράβηξαν άλλους δρόμους και η πλήρης ανυπαρξία ήταν ζητούμενο της ανθρώπινης ύπαρξης, το μηδέν υπήρχε και μπορούσε – ή καλύτερα, έπρεπε – να απεικονιστεί.Φαντάζει παράδοξο ίσως πως κοινωνίες ολόκληρες πορεύτηκαν χωρίς την έννοια του μηδενός, μαθηματικά συστήματα στήθηκαν χωρίς αυτό το μαγικό στρογγυλό σύμβολο.
Οι Βαβυλώνιοι ήταν οι πρώτοι που χρησιμοποίησαν τον μηδέν όχι όμως ως αριθμό αλλά ως δείκτη.
Οι Έλληνες παρά την πρωτοποριακή θεώρηση που έκαναν στα Μαθηματικά δεν είδαν τον μηδέν ούτε ως αριθμό ούτε ως σύμβολο δείκτη για τη θέση των άλλων. Οι αριθμοί που ήταν αναγκαίο να έχουν όνομα ήταν εκείνοι που χρησιμοποιούσαν οι έμποροι και όχι οι μαθηματικοί. Υπήρχαν όμως και εξαιρέσεις και οι εξαιρέσεις αυτές ήταν οι μαθηματικοί αστρονόμοι. Μπορεί ορισμένοι ιστορικοί να υποστήριξαν ότι οι Έλληνες χρησιμοποίησαν το γράμμα όμικρον – αρχικό της λέξης ΟΥΔΕΝ - ως σύμβολο του μηδενός αλλά ο Neugebauer απέρριψε την εικασία υποστηρίζοντας πλην των άλλων ότι οι Έλληνες χρησιμοποιούσαν το όμικρον ως τον αριθμό 70. Πάντως έναν αιώνα μετά Χριστόν, ο Κλαύδιος Πτολεμαίος χρησιμοποιεί το βαβυλωνιακό μηδέν ως δείκτη.
Η ιδέα του μηδενός δείκτη θα κάνει την επανεμφάνισή της στην Ινδία ενώ το έτος 500 ο Aryabhata θα παρουσιάσει ένα σύστημα καταγραφής των αριθμών που θυμίζει το σημερινό αλλά ο μηδέν ως αριθμός δεν υπάρχει.
ΤΟ ΜΗΔΕΝ ΕΡΧΕΤΑΙ ΣΤΗΝ ΕΥΡΩΠΗ. Το 12ο αιώνα μ.Χ. το μηδέν ήρθε και στην Ευρώπη, ύστερα από 600 χρόνια καθυστέρησης! Οι Άραβες, επηρεασμένοι από τους Ινδούς, υιοθέτησαν αμέσως το σύστημά τους και το διέδωσαν στους γύρω λαούς, προσθέτοντας μάλιστα σε αυτό το θαυμαστό λογισμό δικές τους ανακαλύψεις, ιδιαίτερα σημαντικές. Με την επέκτασή τους στην Ευρωπαϊκή ήπειρο, μετέφεραν και αυτές τις μεθόδους τους. Ο Σαμανίδης Μοχάμεντ Ίμπν Μουσσά αλ-Χοβαρεσμί (από το όνομα του οποίου προέκυψε ο όρος αλγόριθμος) έγραψε δύο δοκίμια τα οποία μεταφέρθηκαν στη Δύση. Όμως κάθε εχέφρων και ορθά σκεπτόμενος Ευρωπαίος που ήθελε να χρησιμοποιήσει ή να μεταδώσει την εκπληκτική αυτή γνώση, χρειαζόταν πολύ περισσότερα από αυτά τα δύο βιβλία. Έπρεπε να βρει έναν τρόπο να αντιμετωπίσει τον τρομακτικό συντηρητισμό της δυτικής θρησκείας που έστελνε στη πυρά όποιον τολμούσε να χρησιμοποιήσει τα σύμβολα των «απίστων», δηλαδή τους αριθμούς 1 έως 9. Τα εμπόδια που όρθωσε ο παραλογισμός του θρησκευτικού συντηρητισμού της Ευρώπης διατηρήθηκαν ως το τέλος του Μεσαίωνα και άρχισαν να αίρονται με τις σταυροφορίες από τις οποίες οι Δυτικοί κατακτητές γύρισαν επηρεασμένοι από την παιδεία των Αράβων. Λίγους αιώνες αργότερα, τα γαλλικά και τα γερμανικά πανεπιστήμια, στα οποία μέχρι τον 14ο και τον 15ο αιώνα μ.Χ. μόλις και μετά βίας διδάσκονταν πρόσθεση και αφαίρεση, την περίοδο 1804 - 1851 (Αναγέννηση) χρησιμοποιούσαν πλέον σταθερά το ινδικοαραβικό σύστημα αριθμητικής, που τελικά θριάμβευσε.
Από την μελέτη της ιστορίας των μαθηματικών μπορούμε να διαπιστώσουμε ότι οι αρνητικοί αριθμοί παρά τη γνώση τους δεν νομιμοποιήθηκαν πριν περάσουν αρκετοί αιώνες! Οι αρχαίοι Αιγύπτιοι δεν αναφέρουν τους αρνητικούς αριθμούς. Αντίθετα, οι Έλληνες τους γνώριζαν, με κύριο εκφραστή το Διόφαντο. Τα ελληνικά γεωμετρικά θεωρήματα περιέχουν κανόνες για αρνητικά μεγέθη. Ο Βραχμαγκούπτα αναφέρει τους κανόνες των προσήμων. Όμως οι αρνητικοί αριθμοί δεν "νομιμοποιήθηκαν" αφού δεν θεωρούνταν λύσεις εξισώσεων. Οι Κινέζοι επίσης, δεν αντιμετώπιζαν προβλήματα στους υπολογισμούς θετικών και αρνητικών αφού χρησιμοποιούσαν τον άβακα με δύο ομάδες ράβδων (κόκκινες για τους θετικούς και μαύρες για τους αρνητικούς) (Boyer & Merzbach, 1997).
Η πρώτη εισαγωγή των σημερινών συμβόλων έγινε μόλις το 1489 και στην αρχή χρησιμοποιήθηκαν για να χρεώσουν πλεόνασμα ή έλλειψη των αποθηκών. Η πρώτη συστηματική προσπάθεια εμπέδωσης και μελέτης χρεώνεται στον Cardano Conjectandi στο έργο του Ars. Magna, η δε οριστική τους θεμελίωση επιτεύχθηκε στο 19ο αιώνα με τις συνολοθεωρητικές -αλγεβρικές μεθόδους που γνωρίζουμε (Boyer & Merzbach, 1997
5. Η ιστορία του π
Όταν οι αρχαίοι Βαβυλώνιοι άρχισαν να χτίζουν την πόλη - λέει ο θρύλος- ασχολήθηκαν ιδιαίτερα με τη γεωμετρία. Ήδη από τον 20ό αι. π.Χ. διαπίστωσαν ότι όταν η περιφέρεια οποιουδήποτε κύκλου διαιρείται δια της διαμέτρου του, και το αποτέλεσμα είναι πάντοτε περίπου τρία. Υπολόγισαν μάλιστα την τιμή αυτού του λόγου στα 25/8, τα οποία απέχουν μόλις κατά 0,5% της πραγματικής τιμής του. Πολύ λιγότερο ακριβής είναι η άλλη από τις αρχαιότερες τιμές του η, που συναντάμε στη Βίβλο (Βασιλέων Α, 7, 23), σύμφωνα με την οποία η κυκλική λίμνη του οίκου του Σολομώντα είχε διάμετρο δέκα πήχεις και περιφέρεια τριάντα πήχεις, τοποθετώντας την τιμή ακριβώς στο τρία.
Μία από τις αρχαιότερες και ακριβέστερες τιμές είναι αυτή του αιγυπτίου γραφέα Αχμές. Την έχει καταγράψει σε έναν πάπυρο του Μέσου Βασιλείου, περίπου το 1650 π.Χ., αντιγράφοντας ουσιαστικά έναν ακόμη αρχαιότερο πάπυρο. Ο Αχμές περιέγραψε το π ως το αποτέλεσμα της διαίρεσης του 256 διά του 81, δηλαδή 3,160.
Εκείνος όμως ο οποίος θεωρείται ότι ήταν ο πρώτος που προσέγγισε τον υπολογισμό π σε μια πιο θεωρητική βάση ήταν ο Αρχιμήδης, γι' αυτό και το π είναι γνωστό και ως σταθερά του Αρχιμήδη. Κινέζοι, Ινδοί και Πέρσες σοφοί προσπάθησαν όλοι να υπολογίσουν τη σταθερά αυτή. Ωστόσο, το όνομα με το οποίο τη γνωρίζουμε σήμερα της δόθηκε το 1706, όταν ο ουαλλός μαθηματικός Γουίλιαμ Τζόουνς πρότεινε να ονομαστεί η σταθερά του Αρχιμήδη με το ελληνικό γράμμα π, από τη λέξη "περιφέρεια".
Ωστόσο, οι μεγάλες δυσκολίες με το π τότε δεν είχαν ακόμη αρχίσει. Το 1761 ο Γιόχαν Λάμπερτ απέδειξε ότι το π είναι άρρητος αριθμός. Με απλά λόγια αυτό σημαίνει ότι δεν μπορεί να εκφραστεί ως κλάσμα δύο ακέραιων αριθμών. Στο σχολείο τα παιδιά μαθαίνουν ότι το π είναι περίπου 22/7, η τιμή αυτή είναι όμως και πάλι κατά προσέγγιση, γιατί το π βρίσκεται εκτός μαθηματικής λογικής.
Η δεύτερη μεγάλη ανακάλυψη σημειώθηκε το 1882, όταν ο Φέρντιναντ φον Λίντεμαν απέδειξε ότι το π είχε μία ακόμη ασυνήθιστη ιδιότητα: ήταν υπερβατικός αριθμός. Στη μαθηματική ορολογία αυτό σημαίνει ότι δεν αποτελεί τη ρίζα καμιάς αλγεβρικής εξίσωσης με ρητούς συντελεστές.
Στη μη μαθηματική ορολογία αυτό σημαίνει ότι το π αποτελεί την απόδειξη του παλαιού ρητού ότι δεν μπορεί κανείς να τετραγωνίσει τον κύκλο. Δεν μπορεί δηλαδή κανείς, χρησιμοποιώντας μόνο έναν κανόνα και έναν διαβήτη, να φτιάξει ένα τετράγωνο που να έχει ακριβώς το ίδιο εμβαδόν με έναν δεδομένο κύκλο.
Η κομψότητα της φύσης του π συνοψίζεται όμως στις τόσες προσπάθειες που έχουν γίνει και εξακολουθούν να γίνονται για τη συμπλήρωση των αριθμών του. Η επίμονη αναζήτηση ξεκίνησε ίσως με τον γερμανό μαθηματικό Λούντολφ βαν Τσόιλεν, ο οποίος γύρω στο 1600 υπολόγισε τα πρώτα 35 δεκαδικά ψηφία του π. Ηταν τόσο υπερήφανος γι᾿ αυτό το έργο, στο οποίο αφιέρωσε μεγάλο μέρος της ζωής του, που ζήτησε να γράψουν τα 35 ψηφία στην επιτύμβια στήλη του. Εξίσου επίμονος, ο Γουίλιαμ Σανκς αφιέρωσε από την πλευρά του 20 χρόνια στους υπολογισμούς προχωρώντας το π στα 707 δεκαδικά ψηφία. Δυστυχώς το επίτευγμα του υπέστη τεράστιο πλήγμα όταν οι πρώτο ψηφιακοί υπολογιστές ανακάλυψαν ότι είχε κάνει λάθος στο 528ο δεκαδικό ψηφίο, αχρηστεύοντας όλα τα επόμενα.
Η επέκταση του π στο άπειρο έχει επίσης επανειλημμένως προσελκύσει το ενδιαφέρον των συγγραφέων επιστημονικής φαντασίας. Ο σπουδαίος αμερικανός αστρονόμος Καρλ Σαγκάν στο βιβλίο του "Επαφή" έκρυψε την υπογραφή των εξωγήινων μέσα στα δήθεν τυχαία ψηφία του π, τα οποία στην πραγματικότητα δεν ακολουθούν κάποια συγκεκριμένη διάταξη.
"Ηταν πολύ πονηρό, γιατί αυτό δεν γίνεται" λέει ο καθηγητής Στιούαρτ. "Δεν μπορείς να τακτοποιήσεις το π σε συγκεκριμένη ακολουθία. Ήταν ένα ωραίο απατηλό τέχνασμα εκ μέρους του Σαγκάν. Υπό μίαν έννοιαν ούτε ο ίδιος ο Θεός δεν θα μπορούσε να βρει μια ακολουθία μέσα στο π", πρσοθέτει.
Αεί ο Θεός ο μέγας γεωμετρεί
το κύκλου μήκος ίνα ορίση διαμέτρω
παρήγαγεν αριθμόν απέραντον
και ον φευ! ουδέποτε όλον θνητοί θα εύρωσι.
Αν γράφουμε τους αριθμούς των γραμμάτων που περιέχει κάθε λέξη του πίήματος έχουμε τα πρώτα 22 δεκαδικά ψηφία του π.
6. Ο αριθμός i - H απαρχή των μιγαδικών αριθμών
Ο γιωτ έκανε μια πρώιμη εμφάνιση στη σκηνή της Ιστορίας των Μαθηματικών, τον 16ο αιώνα κατά την εποχή που οι Ιταλοί μαθηματικοί προσπαθούν να βρουν τρόπους για τη λύση τριτοβάθμιων εξισώσεων όπως η x^3 + x = 2.
Το 1572 ο Rafaello Bombelli, ο τελευταίος μεγάλος μαθηματικός της Bologna, παρουσίασε το βιβλίο του Algebra, στο οποίο μελετώντας τις τετραγωνικές ρίζες διάφορων αριθμών σκόνταψε σε ένα αναπάντητο ερώτημα: «Ποια είναι η τετραγωνική ρίζα του αρνητικού αριθμού -1» ; Η λύση γι αυτόν ήταν να «δημιουργήσει» έναν καινούριο αριθμό και θα είναι εξ ορισμού η απάντηση στο ερώτημα «ποια είναι η τετραγωνική ρίζα της αρνητικής μονάδας;».
Το 1572 ο Rafaello Bombelli, ο τελευταίος μεγάλος μαθηματικός της Bologna, παρουσίασε το βιβλίο του Algebra, στο οποίο μελετώντας τις τετραγωνικές ρίζες διάφορων αριθμών σκόνταψε σε ένα αναπάντητο ερώτημα: «Ποια είναι η τετραγωνική ρίζα του αρνητικού αριθμού -1» ; Η λύση γι αυτόν ήταν να «δημιουργήσει» έναν καινούριο αριθμό και θα είναι εξ ορισμού η απάντηση στο ερώτημα «ποια είναι η τετραγωνική ρίζα της αρνητικής μονάδας;».
Βέβαια θα μπορούσε κανείς να αντιτάξει ότι «τέτοιου είδους αριθμός δεν κυκλοφορεί στις γειτονιές της Πραγματικότητας». Όμως υπάρχει αλήθεια αριθμός που να έχει πραγματική υπόσταση; βλέπουμε κανένα 2; πιάνουμε κανένα 14; ακούμε κανένα -5; επομένως όλοι οι αριθμοί είναι κατ’ ουσίαν «φανταστικοί».
Εξάλλου μία ανάλογη απάντηση σε διαφορετικό βέβαια ερώτημα είχε δοθεί από τους Ινδούς μαθηματικούς πριν από αρκετούς αιώνες. Ήταν τότε που η ανάγκη για μία απάντηση στο ερώτημα «με τι ισούται η διαφορά 1-2 ; » είχε οδηγήσει στην επινόηση των αρνητικών αριθμών .
Στη συγκεκριμένη περίπτωση της τετραγωνικής ρίζας του «-1 » μία σημασιακή διεύρυνση της έννοιας αριθμός θα μπορούσε να είναι τέτοια ώστε να χωρέσει και το καινούριο πλάσμα της ανθρώπινης αφαιρετικής σκέψης. Και αυτό συνέβη. Ο Bombelli «έσπρωξε» στο παλκοσένικο της ιστορίας των Μαθηματικών αριθμούς όπως ο R[Om. 9] -στον οποίο το R παριστάνει την τετραγωνική ρίζα και το m το πρόσημο «μείον» και τον οποίο θα συμβολίζαμε σήμερα με Ö(0-9) – .
Ο αλλόκοτος αυτός αριθμός, γέννημα θρέμμα της Ευρώπης, που χαρακτηρίστηκε από τον Descartes «imaginaire» – στην ελληνική γλώσσα «φανταστικός»- έκανε την εμφάνισή του χωρίς να συμβολίζεται με κάποιο γενικώς αποδεκτό σύμβολο. Ο φανταστικός αριθμός γεννήθηκε λοιπόν τον 16ο αιώνα και απέκτησε τον δικό του «παγκόσμιο» συμβολισμό με το γράμμα i τον 18ο αιώνα ύστερα από πρόταση του Euler.
Επόμενο ήταν η δημιουργία ενός νέου συνόλου αριθμών -υποσύνολοτου οποίου είναι το R-, το C, δηλαδή αυτό των μιγαδικών. Οι αριθμοί αυτοί έχουν τη μορφή χ + yi, με τους χ και y να ανήκουν στο R. Οι γνωστοί σε όλους μας λοιπόν πραγματικοί αριθμοί προκύπτουν μηδενίζοντας το φανταστικό μέρος των μιγαδικών, δηλαδή το y, παίρνοντας τη μορφή χ + 0*i = x. Aνίστοιχα οι φανταστικοί προκύπτουν με μηδενισμό του πραγματικού μέρους των μιγαδικών. Αναδιατυπώνουμε λοιπόν, με μαθηματική χροιά, όλοι οι αριθμοί είναι μιγαδικοί!
Το πρόβλημα βέβαια που δημιουργήθηκε είναι ότι όλοι αυτοί οι φανταστικοί και οι μιγαδικοί αριθμοί δεν έχουν θέση στην ευθεία των πραγματικών αριθμών. Οι μαθηματικοί όμως ξεπέρασαν και αυτή τη δυσκολία δημιουργώντας, την ευθεία των φανταστικών αριθμών κάθετη στην ευθεία των πραγματικών αριθμών και από τότε, ενώ οι πραγματικοί εξακολουθούν να κυκλοφορούν στη δική τους ευθεία, οι φανταστικοί «ζουν» πάνω στην άλλη. Όσο για τους μιγαδικούς, αυτοί ζουν στο επίπεδο των δύο αυτών ευθειών.
Οι μιγαδικοί αριθμοί έχουν, μεταξύ άλλων, σημαντικές εφαρμογές στη λύση διαφορικών εξισώσεων αλλά και στη μελέτη διάφορων φυσικών προβλημάτων οπτικής, κυματικής, κβαντομηχανικής και ηλεκτρονικής
7. Ιστορία των εξισώσεων : εδώ
8. ΙΣΤΟΡΙΑ ΤΟΥ ΛΟΓΑΡΙΘΜΟΥ
Τον 16ο – 17ο αιώνα παρατηρήθηκε μια σημαντική ανάπτυξη της επιστημονικής γνώσης σε όλους τους κλάδους. Οι ανακαλύψεις των νέων χωρών, ο γύρος του κόσμου από τον Μαγγελάνο και η ανάπτυξη του ναυτικού εμπορίου δημιούργησαν την ανάγκη παραγωγής χαρτών (Gerhard Mercator, 1596). Η εισβολή των μαθηματικών στην αστρονομία και στη φυσική μετά τον Κοπέρνικο, τον Γαλιλαίο και τον Κέπλερ καθώς και το πλήθος των δεδομένων που προέκυψαν προς επεξεργασία στις προαναφερόμενες επιστήμες, απαιτούσαν από τους επιστήμονες τη διεκπεραίωση περίπλοκων υπολογισμών. Έπρεπε να επινοηθούν τρόποι που θα τους απάλλασσαν από αυτό το βάρος. Και επειδή είναι ευκολότερο να προσθέτουμε παρά να πολλαπλασιάζουμε, βρέθηκε τρόπος μετατροπής της πρόσθεσης σε πολλαπλασιασμό , ο λογάριθμος.
O John Napier (1550-1617), 8ος Λόρδος του Merchistoun στη Σκωτία, γνωστός για τα θρησκευτικού περιεχομένου βιβλία του, ήταν ο πρώτος που, δεχόμενος την πρόκληση μετατροπής μιας πράξης σε μια άλλη πιο απλή, παρατήρησε τη σχέση των όρων μιας γεωμετρικής προόδου και των αντίστοιχων εκθετών τους, που ακολουθούν αριθμητική πρόοδο.
Ο Napier παίρνοντας ως βάση τον αριθμό 1-10-7 υποστήριξε ότι κάθε θετικός αριθμός Ν μπορεί να γραφεί ως Ν=107(1-10-7)L.
Έτσι έχουμε τον πρώτο ορισμό του Νεπέριου λογάριθμου: L=Nap logΝ.
Επί 20 χρόνια συμπλήρωνε τους διαδοχικούς όρους της γεωμετρικής προόδου που κατασκεύασε συγκεντρώνοντας τους τελικά στο έργο του Mirifici Logarithmorum Canonis Descriptio.
Παρατήρηση: Εδώ εμφανίζεται και για πρώτη φορά η τιμή της ακολουθίας
Το χρήμα είναι μαθηματικά
Τον 17ο αιώνα κάποιος ανώνυμος έμπορος ή τοκογλύφος παρατήρησε μια παράξενη συμπεριφορά στην αύξηση του τόκου στις τραπεζικές συναλλαγές, που στηρίζονται σε ανατοκισμό με ετήσιο επιτόκιο διαιρεμένο σε ν ίσα μέρη, όταν ο αριθμός ν είναι πάρα πολύ μεγάλος. Ας παρακολουθήσουμε το φαινόμενο:
Η συνήθης τραπεζική μέθοδος αύξησης του δανειζόμενου κεφαλαίου είναι ο:
Ανατοκισμός
Έστω ότι καταθέτουμε € Κ σε ένα λογαριασμό που αποδίδει ε% ετήσιο επιτόκιο και ανατοκίζεται κάθε χρόνο.
Τέλος του 1ου έτους: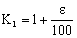
Τέλος του Νου έτους: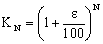
Άλλη συνήθης τραπεζική συναλλαγή είναι ο:
Ανατοκισμός ν φορές τον χρόνο με ετήσιο επιτόκιο διαιρεμένο σε ν ίσα μέρη
Δηλαδή, αν καταθέσουμε € 100 σε ένα λογαριασμό που αποδίδει 5% και τοκίζεται κάθε χρόνο:
Τέλος του 1ου έτους: € 105,00
Αν καταθέτουμε €100 σε ένα λογαριασμό που αποδίδει 5% τον χρόνο και
ανατοκίζεται κάθε εξάμηνο σε ένα χρόνο ανατοκίζεται δύο (2) φορές με επιτόκιο 2,5%
Τέλος 1ου έτους: 105,06
ανατοκίζεται κάθε τρίμηνο σε ένα χρόνο ανατοκίζεται τέσσερις (4) φορές με επιτόκιο 1,66%
Τέλος 1ου έτους: 105,09 €
ανατοκίζεται κάθε μήνα σε ένα χρόνο ανατοκίζεται δώδεκα (12) φορές με επιτόκιο
0,416%.
Τέλος 1ου έτους: 105,12 €
ανατοκίζεται κάθε ημέρα σε ένα χρόνο ανατοκίζεται τριακόσιες εξήντα
πέντε (365) φορές με επιτόκιο 0,0137 %
Τέλος 1ου έτους: 105,19 €
Έστω ότι ο ανατοκισμός γίνεται ν φορές τον χρόνο. Για κάθε περίοδο μετατροπής ως επιτόκιο θεωρείται το ετήσιο επιτόκιο διαιρεμένο με τον ν, δηλαδή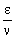 
%.
Τέλος 1ου έτους: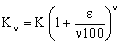
Παρατήρηση: Το τελικό κεφάλαιο για περίοδο μετατροπής πάρα πολύ μικρή, π.χ.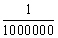 
/ 
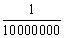, δεν ξεπερνά το 2,72 του αρχικού κεφαλαίου.
Παρατηρούμε ότι ο τύπος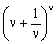 
πλησιάζει μια τιμή χωρίς να τη φτάνει και αυτή είναι ο αριθμός e. Τότε λέμε ότι η ακολουθία με τύπο 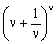έχει όριο τον αριθμό e.
Το e ως όριο
Ο αριθμός e, όπως διαπιστώσαμε, είναι όριο της ακολουθίας.
Αλλά, αφού για μεγάλες τιμές του ν η τιμή του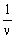 
θα είναι σχεδόν μηδέν,
έχουμε: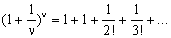 
Συνεπώς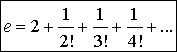 
Ο τετραγωνισμός της υπερβολής
O Gregorius de Saint-Vincent (1584-1667), στην προσπάθεια τετραγωνισμού της υπερβολής, διαπιστώνει ότι, αν οι τετμημένες της γραφικής παράστασης της συνάρτησης μεταβάλλονται με γεωμετρική πρόοδο, τότε το εμβαδόν που βρίσκεται μεταξύ του άξονα των τετμημένων και της υπερβολής μεταβάλλεται με αριθμητική πρόοδο..
Όταν το e συναντά το φ: Λογαριθμική έλικα
Ο Jacob Bernoulli (1654-1705) μελέτησε τη λογαριθμική έλικα και την ονόμασε spira mirabilis λόγω των σπανίων μαθηματικών ιδιοτήτων της, που την καθιστούν, μετά τον κύκλο, το πιο προσφιλές διακοσμητικό μοτίβο.
Η λογαριθμική έλικα περιγράφεται ως καμπύλη με αφετηρία ένα σημείο (τον πόλο) και ανελίσσεται με τρόπο ώστε η απόσταση των σημείων της από το πόλο να αυξάνει με γεωμετρική πρόοδο, εφόσον η γωνία περιστροφής αυξάνει με αριθμητική πρόοδο. Κάθε ευθεία που διέρχεται από τον πόλο τέμνει την έλικα υπό την ίδια γωνία.
Οι λογάριθμοι
Η ιδέα των λογαρίθμων γεννήθηκε πιθανόν από τους αστρονόμους οι οποίοι έπρεπε να πολλαπλασιάζουν και να διαιρούν πολύπλοκες τριγωνομετρικές ποσότητες. Στο μεταξύ οι πίνακες με τους αριθμούς και τις δυνάμεις έδειχναν ότι ο πολλαπλασιασμός στον ένα πίνακα αντιστοιχούσε σε πρόσθεση στον άλλο. Στην αυγή του 17ου αιώνα ο σκωτσέζος John Napier ή Neper είχε την ιδέα της δημιουργίας ενός πίνακα λογαρίθμων ο οποίος θα διευκόλυνε τους πολλαπλασιασμούς οποιωνδήποτε ποσοτήτων ανάγοντάς τους σε προσθέσεις. Το 1617 δημοσίευσε τον σχετικό πίνακα και το όνομά του δημιούργησε αργότερα τον όρο “νεπέριοι λογάριθμοι”.
Σήμερα η έννοια λογάριθμος έχει διαφοροποιηθεί σε σχέση με εκείνη που πρότεινε Οο Neper. O λογάριθμος ενός αριθμού, όπως λόγου χάρη ο 50, είναι ο ΕΚΘΕΤΗΣ τον οποίο πρέπει να έχει o αριθμός e ( βάση ) ώστε να είναι ίσος με 50. eln50 = 50.
9. ο «ασύλληπτος» αριθμός e
10. Ελληνικά Μαθηματικά : εδώ
11 Κωνσταντίνος Καραθεοδωρής
Αξιόλογος διεθνώς Έλληνας μαθηματικός των αρχών του 20ου αιώνα (γνωστό το θεώρημα Καραθεοδωρή στην θεωρία μέτρου ). Προσωπικός φίλος και συνεργάτης του Αϊστάιν. Ο τελευταίος εκφράστηκε με κολακευτικά λόγια για τον Έλληνα μαθηματικό. Σώζεται αλληλογραφία μεταξύ των δύο κορυφαίων επιστημόνων. Εκεί φαίνεται ο θαυμασμός του Αϊστάιν για τον Καραθεοδωρή.
" Αν θέλετε να μπείτε στον κόπο να μου εξηγήσετε ακόμα και τους κανονικούς μετασχηματισμούς θα βρείτε έναν ευγνώμονα και ευσυνείδητο ακροατή. Αν όμως λύσετε και το πρόβλημα των κλειστών γραμμών του χρόνου, θα σταθώ μπροστά σας με σταυρωμένα χέρια. Πίσω από αυτό υπάρχει κρυμμένο κάτι που είναι αντάξιο του ιδρώτα των καλυτέρων."
Στην παρακάτω ιστοσελίδα φίλων του Καραθεοδωρή θα βρείτε πολλά στοιχεία για τη ζωή και το έργο του : http://www.karatheodori.gr/
12. ΘΑΛΗΣ ο ΜΙΛΗΣΙΟΣ
'Eζησε στο διάστημα (640-546 π.Χ.). θεωρείται ο πατέρας των μαθηματικών. σε αυτόν η μαθηματική επιστήμη χρωστά την πρώτη απόδειξη. Θεμελίωσε την αποδεικτική μέθοδο. Η πρώτη απόδειξη στην ιστορία των μαθηματικών οφείλετε σ΄αυτόν και αφορά την πρόταση :
" Η διάμετρος ενός κύκλου τον χωρίζει σε δύο ίσα μέρη".
" Η διάμετρος ενός κύκλου τον χωρίζει σε δύο ίσα μέρη".
Οι ενασχολήσεις αυτές οδήγησαν στην ανάπτυξη της Ελληνικής Θεωρητικής Γεωμετρίας και στην απόσπασή της από το σύνολο των εμπειρικών γνώσεων των τεχνών της ζωής.
13. ΤΑ ΣΤΟΙΧΕΙΑ ΤΟΥ ΕΥΚΛΕΙΔΗ
Μετά τον θάνατο του Μ. Αλεξάνδρου ένας από τους διαδόχους του ο Πτωλεμαίος όρισε ως πρωτεύουσα της μακεδονικής αυτοκρατορίας την Αλεξάνδρεια της Αιγύπτου. Στην Αλεξάνδρεια γεννήθηκε ο σπουδαίος έλληνας μαθηματικός Ευκλείδης ο Αλεξανδρεύς. Πιθανώς φοίτησε στην Ακαδημία του Πλάτωνα στην Αθήνα. Όταν επί Πτωλεμαίου ιδρύθηκε το Πανεπιστήμιο της Αλεξάνδρειας ο Ευκλείδης ορίστηκε ως καθηγητής και στέλεχος του. Με αφορμή τα νέα του καθήκοντα συγγράφει το περίφημο βιβλίο γεωμετρίας : Τα στοιχεία του Ευκλείδη. Το βιβλίο αποτελείται από 13 μέρη ( κεφάλαια). Συνενώνει τις μέχρι τότε γνώσεις στην γεωμετρία. Το σημαντικότερο όμως είναι η αξιωματική θεμελίωση του εγχειριδίου. Αποτελεί τον πρώτο αξιόλογο τρόπο επιστημονικής συγκρότησης της γεωμετρίας. Αυτό κάνει τα στοιχεία του Ευκλείδη ένα από τα σημαντικότερα βιβλία γεωμετρικής σκέψης. Στην περίοδο της αναγέννησης τυγχάνει πολλαπλών εκδόσεων και συστηματικής μελέτης. Το λεγόμενο πέμπτο αξίωμα του Ευκλείδη μελετάται ως προς την ανεξαρτησία του. Από εδώ αργότερα θα πηγάσουν οι λεγόμενες μη - ευκλείδειες γεωμετρίες.
Είναι το δεύτερο βιβλίο μετά την βίβλο που έχει εκδοθεί σε περισσότερα αντίτυπα παγκοσμίως όλους τους αιώνες. Για το λόγο αυτό χαρακτηρίζεται ως : Η βίβλος των μαθηματικών.
Ας δούμε μερικά αποσπάσματα από το αρχαίο κείμενο :
α΄ [1]. Σημεῖόν ἐστιν, οὗ μέρος οὐθέν.
β΄ [2]. Γραμμὴ δὲ μῆκος ἀπλατές.
ια΄ [11]. Ἀμβλεῖα γωνία ἐστὶν ἡ μείζων ὀρθῆς.
ιε΄ [15]. Κύκλος ἐστὶ σχῆμα ἐπίπεδον ὑπὸ μιᾶς γραμμῆς περιεχόμενον [ἣ καλεῖται περιφέρεια], πρὸς ἣν ἀφ' ἑνὸς σημείου τῶν ἐντὸς τοῦ σχήματος κειμένων πᾶσαι αἱ προσπίπτουσαι εὐθεῖαι [πρὸς τὴν τοῦ κύκλου περιφέρειαν] ἴσαι ἀλλήλαις εἰσίν.
ις΄ [16]. Κέντρον δὲ τοῦ κύκλου τὸ σημεῖον καλεῖται.
ιζ΄ [17]. Διάμετρος δὲ τοῦ κύκλου ἐστὶν εὐθεῖά τις διὰ τοῦ κέντρου ἠγμένη καὶ περατουμένη ἐφ' ἑκάτερα τὰ μέρη ὑπὸ τῆς τοῦ κύκλου περιφερείας, ἥτις καὶ δίχα τέμνει τὸν κύκλον.
ιη΄ [18]. Ἡμικύκλιον δέ ἐστι τὸ περιεχόμενον σχῆμα ὑπό τε τῆς διαμέτρου καὶ τῆς ἀπολαμβανομένης ὑπ' αὐτῆς περιφερείας. κέντρον δὲ τοῦ ἡμικυκλίου τὸ αὐτό, ὃ καὶ τοῦ κύκλου ἐστίν.
κβ΄ [22]. Τῶν δὲ τετραπλεύρων σχημάτων τετράγωνον μέν ἐστιν, ὃ ἰσόπλευρόν τέ ἐστι καὶ ὀρθογώνιον, ἑτερόμηκες δέ, ὃ ὀρθογώνιον μέν, οὐκ ἰσόπλευρον δέ, ῥόμβος δέ, ὃ ἰσόπλευρον μέν, οὐκ ὀρθογώνιον δέ, ῥομβοειδὲς δὲ τὸ τὰς ἀπεναντίον πλευράς τε καὶ γωνίας ἴσας ἀλλήλαις ἔχον, ὃ οὔτε ἰσόπλευρόν ἐστιν οὔτε ὀρθογώνιον: τὰ δὲ παρὰ ταῦτα τετράπλευρα τραπέζια καλείσθω.
κγ΄ [23]. Παράλληλοί εἰσιν εὐθεῖαι, αἵτινες ἐν τῷ αὐτῷ ἐπιπέδῳ οὖσαι καὶ ἐκβαλλόμεναι εἰς ἄπειρον ἐφ' ἑκάτερα τὰ μέρη ἐπὶ μηδέτερα συμπίπτουσιν ἀλλήλαις.
δ΄.[4]
Ἐὰν δύο τρίγωνα τὰς δύο πλευρὰς [ταῖς] δυσὶ πλευραῖς ἴσας ἔχῃ ἑκατέραν ἑκατέρᾳ καὶ τὴν γωνίαν τῇ γωνίᾳ ἴσην ἔχῃ τὴν ὑπὸ τῶν ἴσων εὐθειῶν περιεχομένην, καὶ τὴν βάσιν τῇ βάσει ἴσην ἕξει, καὶ τὸ τρίγωνον τῷ τριγώνῳ ἴσον ἔσται, καὶ αἱ λοιπαὶ γωνίαι ταῖς λοιπαῖς γωνίαις ἴσαι ἔσονται ἑκατέρα ἑκατέρᾳ, ὑφ' ἃς αἱ ἴσαι πλευραὶ ὑποτείνουσιν.
ε΄.[5]
Τῶν ἰσοσκελῶν τριγώνων αἱ πρὸς τῇ βάσει γωνίαι ἴσαι ἀλλήλαις εἰσίν, καὶ προσεκβληθεισῶν τῶν ἴσων εὐθειῶν αἱ ὑπὸ τὴν βάσιν γωνίαι ἴσαι ἀλλήλαις ἔσονται.
Εκτεταμένα αποσπάσματα των Στοιχείων βρίσκουμε εδώ:
14 Πειραματική γεωμετρία
Ενδιαφέροντα ιστορικά στοιχεία για την πειραματική γεωμετρία και την κατασκευή εργαλείων καθώς και για την διδακτική τους αξιοποίηση με μορφή δραστηριοτήτων υπαρχουν εδώ.
15. Μη ευκλείδειες γεωμετρίες
Ο μύθος του Ευκλείδη.
" Η ευκλείδεια γεωμετρία περιέχει τις μόνες αληθινές εποπτείες γιατί ταιριάζει απόλυτα με την εμπειρική μας πραγματικότητα".
Υπερβολικό παραβολοειδές.
Ψευδοσφαίρα.
" Καμμία γεωμετρία δεν είναι περισσότερο αληθινή. Είναι απλά πιο βολική ".
Ανρί Πουανκαρέ. Γάλλος μαθηματικός
Οι πρωτοπόροι των μη ευκλείδειων γεωμετριών :
János Bolyai
N. I. Lobachevsky
Bernhard Riemann
ΧΡΗΣΙΜΕΣ ΣΥΝΔΕΣΕΙΣ
1. Eνδιαφέρον ντοκιμαντέρ για την χρήση των μη ευκλείδειων γεωμετριών στην μελέτη του σύμπαντος υπάρχει από την εκπομπή της ΕΤ3 : " Το Σύμπαν που αγάπησα" με τον Επίκουρο καθηγητή αστροφυσικής Μάνο Δανέζη. Παρακολουθείστε το video :
2. Εμπεριστατωμένη διατριβή στην ιστορία των μη ευκλείδειων γεωμετριών εδώ
3. Αρκετά στοιχεία και εδώ
16. ΤΑ 3 ΑΛΥΤΑ ΠΡΟΒΛΗΜΑΤΑ
ΤΗΣ ΕΛΛΗΝΙΚΗΣ ΑΡΧΑΙΟΤΗΤΑΣ
Όταν οι αρχαίοι Έλληνες ήθελαν να λύσουν ένα πρόβλημα προσπαθούσαν αρχικά να το λύσουν κάνοντας χρήση των πιο απλών καμπυλών, των κύκλων και των ευθειών δηλαδή χρησιμοποιώντας μόνο κανόνα και διαβήτη. Όταν λοιπόν δεν μπορούσαν να λύσουν κάποιο πρόβλημα με αυτές της συνθήκες τότε το θεωρούσαν άλυτο και προσπαθούσαν να το λύσουν κάνοντας χρήση άλλων πιο πολύπλοκων καμπυλών. Έτσι τα “3 Άλυτα Μαθηματικά Προβλήματα Της Αρχαιότητας” δεν μπορούν να λυθούν με κανόνα και διαβήτη άλλα υπάρχουν αρκετές λύσεις αιτών με άλλες καμπύλες.
Το δήλιο πρόβλημα ή ο διπλασιασμός του κύβου απασχόλησε τους αρχαίους Έλληνες γεωμέτρες και η αναζήτηση λύσεων, οδήγησε σε μια έντονη ανάπτυξη της Γεωμετρίας.
Το δήλιο πρόβλημα απόκτησε δημοσιότητα όταν το ανέφερε, σε μια τραγωδία o βασιλιάς της Κρήτης Μίνως διαμαρτυρόμενος γιατί το κενοτάφιο, που προοριζόταν για το γυιό του Γλαύκο, ήταν πολύ μικρό για βασιλικό μνημείο και απαιτούσε το διπλασιασμό του όγκου του χωρίς να αλλάξει το κυβικό του σχήμα. Πανελλήνια γνωστό όμως έγινε το πρόβλημα αυτό όταν αναφέρθηκε από το μαντείο του Δήλιου Απόλλωνα, όταν δηλαδή ρωτήθηκε το μαντείο, τι πρέπει να κάνουν για να απαλλαγούν από το λοιμό που μάστιζε το νησί Δήλο, απάντησε ότι τούτο θα συμβεί αν διπλασιάσουν τον κυβικό βωμό του Απόλλωνα. Έτσι το πρόβλημα του διπλασιασμού του κύβου πέρασε στην ιστορία με το όνομα “Δήλιο πρόβλημα”.
Οι λύσεις που δόθηκαν στο πρόβλημα, κατά την ελληνική αρχαιότητα, σώθηκαν και φθάσανε σε μάς από τον σχολιαστή των έργων του Αρχιμήδη Ευτόκιο (6 αι. μ.χ). Αυτός σχολιάζοντας ανάλογο πρόβλημα του Αρχιμήδη και τη μέθοδο που αυτός χρησιμοποίησε για να το λύσει, δίνει όλες τις λύσεις παρεμβολής που του ήταν τότε γνωστές από παλαιότερες συγγραφές.
Σήμερα δεν γνωρίζουμε κάτω από ποιες συνθήκες τέθηκε το πρόβλημα της τριχοτόμησης γωνίας στην ελληνική αρχαιότητα. Ξέρουμε όμως ότι αποτελούσε το ένα από τα τρία μεγάλα προβλήματα μετά το Δήλιο και τον τετραγωνισμό του κύκλου. Ουσιαστικά το πρόβλημα έγκειται στην τριχοτόμηση οξείας γωνίας, διότι αν είναι αμβλεία αφαιρούμε απο αυτήν την ορθή που μπορεί να τριχοτομηθεί με χάρακα και διαβήτη. Η τριχοτόμηση όμως μιάς οξείας γωνίας είναι αδύνατο να πραγματοποιηθεί μόνο με χάρακα και διαβήτη γιατί η εξίσωση που την εκφράζει είναι τρίτου βαθμού χωρίς να μπορεί να αναχθεί σε δευτέρου. Πράγματι από τη τριγωνομετρία μας είναι γνωστή η σχέση στην οποία αν θέσουμε εφ3θ=α και εφθ=x και κάνουμε τις πράξεις θα φθάσουμε στη x3-3αx2-3x+α=0 που είναι η εξίσωση της τριχοτόμησης. Η κατασκευή με χάρακα και διαβήτη των ριζών αυτής της εξίσωσης είναι δυνατή μόνο αν μπορεί αυτή να αναλυθεί σε δύο παράγοντες, ένα πρωτοβάθμιο και ένα δευτεροβάθμιο, όμως αυτό αποδείχθηκε μόλις το 1837, ότι είναι αδύνατο.
Οι αρχαίοι Έλληνες γεωμέτρες όταν οι προσπάθειές τους με το χάρακα και το διαβήτη δεν απέδωσαν, στράφηκαν σε άλλες καμπύλες εκτός του κύκλου και σε άλλες μεθόδους. Το πρώτο αποτέλεσμα αυτής της προσπάθειας ήταν η επινόηση από τον Ιππία τον Ηλείο της πρώτης καμπύλης στην ελληνική Γεωμετρία, μετά την περιφέρεια, της τετραγωνίζουσας, με τη βοήθεια της οποίας έδωσε και τη πρώτη λύση του προβλήματος.
Οι γνωστότεροι αρχαίοι γεωμέτρες που ασχοληθήκανε με το πρόβλημα της τριχοτόμησης της γωνίας ειναι :
- Ο Ιππίας ο Ηλείος (περίπου 430 π.χ)
- Ο Αρχιμήδης (287-212 π.χ)
- Ο Νικομήδης (περίπου 200 π.χ)
- Ο Πάππος ο Αλεξανδρινός (3ος αι. μ.χ)
Η μέτρηση του εμβαδού του περικλειομένου από κάποιο σχήμα, ήταν σε όλους τους λαούς, από την εποχή που ακόμη η γεωμετρία ήταν εμπειρικής μορφής, βασική επιδίωξη όλων των γεωμετρών. Από τη στιγμή που διαλέξανε σαν μονάδα μέτρησης των εμβαδών, το τετράγωνο με πλευρά τη μονάδα μήκους, αυτόματα τέθηκε και το πρόβλημα του τετραγωνισμού των διαφόρων σχημάτων.
Αρχικά “τετραγωνίστηκαν” δηλαδή προσδιορίστηκε το εμβαδόν τους, τα ορθογώνια, τα τρίγωνα, τα παραλληλόγραμμα και ορισμένα πολύγωνα. Μετά από αυτό ήταν φυσικό να επιδιωχθεί και ο τετραγωνισμός σχημάτων περικλειομένων από καμπύλες γραμμές και πρώτου από όλα του κύκλου. Ο τετραγωνισμός του κύκλου, το τρίτο από τα μεγάλα προβλήματα της αρχαιότητας, απασχόλησε πολλούς ερευνητές για πολλούς αιώνες και υπήρξε το μεγάλο εμπόδιο πάνω στο οποίο σκόνταψαν μεγάλα ονόματα.
Η απαίτηση του προβλήματος είναι να κατασκευαστεί τετράγωνο ισοδύναμο με δοσμένο κύκλο, αν δηλαδή είναι R η ακτίνα του κύκλου και x η ζητούμενη πλευρά του τετραγώνου, πρέπει να αληθεύει η σχέση , όπου π ο λόγος του μήκους της περιφέρειας προς το μήκος της διαμέτρου του κύκλου. Παρόλο που εμπειρικά είχε διαπιστωθεί ότι ο λόγος π της περιφέρειας προς τη διάμετρο διατηρείται σταθερός, ωστόσο η κατασκευή αυτού του λόγου και όταν ακόμη η Γεωμετρία εφοδιασμένη με την απόδειξη είχε γίνει επιστήμη, στάθηκε αδύνατη. Υπήρξαν κατασκευές του π μεγαλοφυείς κατά τη σύλληψη όχι όμως πραγματοποιημένες σύμφωνα με την απαίτηση του “χάρακα και του διαβήτη” που έθεταν τότε. Παράλληλα έγιναν μεγαλειώδεις προσπάθειες υπολογισμού της τιμής του π, οι οποίες με πρωτεργάτη τον Αρχιμήδη, έδωσαν ένδοξα αποτελέσματα.
Ο πρώτος που ασχολήθηκε με τον τετραγωνισμό του κύκλου είναι οΑναξαγόρας ο Κλαζομένιος (500-428 π.χ) δάσκαλος και φίλος του Περικλή. Στη συνέχεια ασχολήθηκαν οι Ιπποκράτης ο Χίος (470- 400 π.χ) ο σοφιστήςΑντιφών ο Αθηναίος (περί το 430 π.χ) ο επίσης σοφιστής Βρύσων ο Ηρακλειώτης σύγχρονος του Αντιφώντα. Ουσιαστική ώθηση στο πρόβλημα του τετραγωνισμού του κύκλου, δόθηκε από τον σοφιστή Ιππία τον Ηλείο (β’ μισό του 5ου αι. π.χ) και από τους Πάππο (3ος αι. μ.χ) και τον Δεινόστρατο (4ος αι. π.χ) αδελφό του Μέναιχμου.
Ο Ιάμβλιχος (250-325 μ.χ) αναφέρει ότι τον τετραγωνισμό του κύκλου κατόρθωσαν :
- O Αρχιμήδης (267-212 π.χ) με τη βοήθεια της “Έλικας”.
- Ο Νικομήδης (περίπου 200 π.χ) με την καμπύλη που ονομαζόταν “ιδίως τετραγωνίζουσα”.
- Ο Απολλώνιος (265-170 π.χ) με την καμπύλη που ονόμαζε ο ίδιος “αδελφή της κοχλοειδούς” που ήταν όμως ίδια με την καμπύλη του Νικομήδη.
- Ο Κάρπος με κάποια καμπύλη την οποία ονομάζει απλά “εκ διπλής κινήσεως προερχομένη”.
Και άλλοι πολλοί !!
Πηγή: telemath.gr
17 Ιστορικά προβλήματα γεωμετρίας του Θαλή Μιλήσιου.
18. IΣΤΟΡΙΑ ΤΟΥ ΠΥΘΑΓΩΡΕΙΟΥ ΘΕΩΡΗΜΑΤΟΣ
Μπορείτε να βρείτε εμπεριστατωμένη ιστορία του πυθαγωρείου θεωρήματος εδώ.
19. Συνοπτική ιστορία της τριγωνομετρίας εδώ.
20. Συνοπτική ιστορία των αρχαιοελληνικών μαθηματικών
21. ΠΙΝΑΚΑΣ ΑΝΑΠΤΥΞΗΣ ΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ
3000-2000 π.Χ
Αίγυπτος
|
Εμφάνιση ιερογλυφικών αριθμών
Κατασκευή πυραμίδων |
Κίνα
|
Πραγματεία Μεταθέσεων
Πραγματεία αριθμητικής σε 9 κεφάλαια ( υπολογισμοί εμβαδών)
Προσέγγιση της τιμής του π
|
Μεσοποταμία
|
Εμφάνιση σφηνοειδούς γραφής των αριθμών
|
2000-1000 π.Χ
Αίγυπτος
|
Πάπυροι Rhind και Μόσχας
Υπολογισμοί όγκων και εμβαδών |
Μεσοποταμία
|
Υπολογισμοί εμβαδών και "επίλυση" εξισώσεων β΄ βαθμού
|
1000-500 π.Χ
Ελλάδα
|
Θαλής. Έννοια απόδειξης, Αποδεικτική Γεωμετρία
Πυθαγόρας -Πυθαγόρειοι. Θεωρία Αριθμών, γεωμετρία, μουσική κλίμακα |
Ινδία
|
Υπολογισμός τετραγωνικών ριζών
|
500-300 π.Χ
Ελλάδα
|
Οινοπίδης ο Χίος: Γεωμετρία
Ιπποκράτης ο Χίος: Τετραγωνισμός Ζήνων ο Ελεάτης: Παράδοξα κίνησης ( που περικλείουν έννοιες συνέχειας και ορίου) Λεύκιππος: Ατομική θεωρία Αντιφών: Μέθοδος εξάντλησης Ιππίας ο Ηλείος: Τετραγωνισμός Θεόδωρος ο Κηρυναίος: Ασύμμετρους αριθμούς Δημόκριτος: Ατομική Θεωρία, Γεωμετρία Αρχύτας: Αναλογίες Πλάτων: Θεμελίωση Μαθηματικών Θεαίτητος: Γεωμετρία Εύδοξος: Αναλογίες Μέναιχμος: Κωνικές Δεινόστρατος: Τετραγωνίζουσα Αριστοτέλης: Λογική Ευκλείδης: Στοιχεία, Δεδομένα, Φαινόμενα |
300-0 π.Χ
|
Ελλάδα
|
Αρίσταρχος: Πρώτη διατύπωση της θεωρίας του ηλιοκεντρικού συστήματος
Ερατοσθένης: Πρώτοι αριθμοί, Γεωδαισία Απολλώνιος: Κωνικές Αρχιμήδης: Γεωμετρία, Αρχές απειροστικού λογισμού, Θεωρητική φυσική, Εφαρμογές Ίππαρχος: Αστρονομία, Τριγωνομετρία Σωσιγένης: Δημιουργία Ιουλιανού ημερολογίου |
Κίνα
|
Τετραγωνικές, κυβικές ρίζες. Γραμμικές εξισώσεις
|
0-200 μ.Χ
|
Ελλάδα
|
Ήρων ο Αλεξανδρεύς: Γεωδαισία, Μαθηματικά, Εφαρμογές
Σερήνος: Κυλινδρικές τομές Νικόμαχος: Θεωρία Αριθμών Θέων ο Σμυρναίος: Θεωρία Αριθμών Κλαύδιος Πτολεμαίος: Αστρονομία, Τριγωνομετρία, Γεωδαισία |
Κίνα
|
Αστρονομία, Γεωμετρία
|
200-400 μ.Χ
Ελλάδα
|
Διόφαντος: Άλγεβρα, Θεωρία Αριθμών
Πάππος: Γεωμετρία Ιαμβλίχος: Θεωρία Αριθμών Θέων ο Αλεξανδρεύς: Γεωμετρία |
Κίνα
|
Liu Hui: Τεχνικές μέτρησης. Αριθμητική
|
400-800 μ.Χ
Ελλάδα
|
Υπατία: Γεωμετρία, Αστρονομία
Πρόκλος: Γεωμετρία |
Μεξικό
|
Ανάπτυξη της αρίθμησης και αστρονομίας των Maya
|
Μέση Ανατολή
|
Με τον Χαρούν αλ Ρασίντ , προστάτη των Μαθηματικών, (βασίλευσε 786-808) αρχίζει η αραβική εποχή, αμάλγαμα δύο κόσμων (ελληνικού - αραβικού)
|
Ινδία
|
Aryabhata και Τριγωνομετρία
Brahmagupta και απροσδιόριστη ανάλυση, ανάπτυξη του ινδοαραβικού συστήματος αρίθμησης |
Ιταλία
|
Boethius: Γεωμετρία και Θεωρία Αριθμών
|
Κίνα
|
Αριθμητική, Μέτρηση κύκλου, Εξισώσεις 3ου βαθμού, Αστρονομία
|
800-1000 μ.Χ
|
Μέση Ανατολή
|
al Khowârismi: Άλγεβρα
Honein ibn Ishâq: Ελληνικά Μαθηματικά Tâbt ibn Qurra: Κωνικές, Ελληνικά Μαθηματικά Abû Kâmil: Γεωμετρία, Άλγεβρα Al Nairizi: Γεωμετρία Αβικέννας: Γεωμετρία, Αριθμητική |
Ινδία
|
Mahâvira: Αριθμητική, Άλγεβρα
|
Ισπανία
|
Gerbert (Sylvester II): Αριθμητική
|
1000-1200 μ.Χ
Βυζάντιο
|
Μιχαήλ Ψελλός: Αστρονομία
|
Περσία
|
Ομάρ Καγιάμ: Γεωμετρική λύση κυβικών εξισώσεων, αίτημα των παραλλήλων, θεωρία αναλογιών
|
Ινδία
|
Al Biruni: Σφαιρική τριγωνομετρία
Bhâskara: Άλγεβρα |
Ισπανία
|
Αραβικά έργα μεταφράζονται σε λατινικά
Abraham ben Ezra: Συνδυαστική |
Ιταλία
|
Μεταφράσεις αραβικών έργων στα λατινικά (Πλάτων του Tivoli, Gerardo της Gremoma)
|
Κίνα
|
Αριθμητική
|
1200-1400 μ.Χ
Αγγλία
|
Μελέτη κίνησης, επιτάχυνσης
Calculatores |
Βυζάντιο
|
Ιωάννης Παχυμέρης: Περί των τεσσάρων μαθημάτων
Παχυμερούς μεγάλου διδασκάλου: (Αριθμητική, μουσική, Γεωμετρία, Αστρονομία) Μάξιμος Πλανούδης: Θεωρία Αριθμών Εμμανουήλ Μοσχόπουλος: Μαγικά τετράγωνα Νικόλαος Ραβδάς: Αριθμητική, Γεωμετρία |
Γαλλία
|
O Jordanus και προχωρημένη Άλγεβρα
|
Ιταλία
|
Leonardo της Πίζας (FIbonacci): Άλγεβρα, Αριθμητική, Γεωμετρία ( εισαγωγή αραβικών γνώσεων)
|
Κίνα
|
Επίλυση πολυωνυμικών εξισώσεων
|
Περού
|
Κίπους: ( κόμβοι σε σχοινιά ) για μέτρηση
|
Περσία
|
Nasir al Din Tusi και τριγωνομετρία
|
1400-1600 μ.Χ
Αγγλία
|
Τριγωνομετρία
|
Γαλλία
|
Ο Vieta και ο αλγεβρικός συμβολισμός
|
Γερμανία
|
Reichenmeisters: Προοπτική (Durer)
|
Ιταλία
|
Αλγεβρική επίλυση εξισώσεων 3ου βαθμού (Ferrari, Tartaglia, Carnano ). Γεωμετρία, Γεωμετρική προοπτική
|
Ινδία
|
Υπολογισμοί ημx , συνx
|
Κάτω Χώρες
|
Stevin και τα δεκαδικά κλάσματα
|
Πορτογαλία
|
N. Nuñez (Άλγεβρα, Γεωμετρία, Ναυσιπλοΐα
|
1600-1700 μ.Χ
|
Ευρώπη
|
Kepler, Newton: Ουράνια μηχανική
Descartes-Fermat: Δημιουργία Αναλυτικής Γεωμετρίας Napier, Briggs: Ανακάλυψη λογαρίθμων Girard-Descartes: Θεωρία εξισώσεων Pascal-Fermat: Θεωρία πιθανοτήτων Fermat-Pascal: Θεωρία Αριθμών Pascal-Desargues: Προβολική Γεωμετρία Newton-Leibniz: Δημιουργία απειροστικού λογισμού Γαλιλαίος: Γεωμετρία, Αστρονομία, Μηχανική Huygens: Γεωμετρία, Φυσική, Αστρονομία, Θεωρία πιθανοτήτων. |
Κίνα
|
Ο Mateo Ricci μεταφράζει τα στοιχεία του Ευκλείδη στα κινέζικα.
|
1700-1800 μ.Χ
Ανάπτυξη τεχνικής για την επίλυση διαφορικών εξισώσεων (Euler, D`Alembert, Clairaut, Bernoulli, Lagrange)-Προσπάθεια αυστηρής θεμελίωσης του απειροστικού λογισμού (D`Alembert, Euler, Lagrange)-Θεωρία πιθανοτήτων (Bernoulli, de Moivre, Bayes, Laplace )-Eπίλυση πολυωνυμικών εξισώσεων (Lagrange, Ruffini)-Γεωμετρία: Μελέτη Καμπυλών (Euler, Clairaut, Monge, Dupin)-Λογισμός Μεταβολών (Euler, Lagrange)
1800-1900 μ.Χ
Αλγεβρική Θεωρία αριθμών-Θεωρία Galois-Ομάδες και Σώματα-Quaternions και οι μη μεταθετικές άλγεβρες-Θεωρία Πινάκων-Η αριθμητικοποίηση της ανάλυσης-Διαφορική Γεωμετρία-Μη Ευκλείδειες Γεωμετρίες-Προβολική Γεωμετρία-Διανυσματική Ανάλυση-Θεμελίωση της Γεωμετρίας-Μαθηματική Λογική-Θεωρία πιθανοτήτων-Θεωρία Συναρτήσεων
1900-1999 μ.Χ
Θεωρία Συνόλων-Ανάπτυξη της Τοπολογίας-Αυστηρή Θεμελίωση της Θεωρίας Πιθανοτήτων-Επίδραση των Η/Υ στα Μαθηματικά-Αλγεβροποίηση των Μαθηματικών-Επίλυση ανοιχτών προβλημάτων (το τελευταίο θεώρημα του Fermat, το πρόβλημα των 4 χρωμάτων)-Η γένεση της ομάδας N. Bourbaki-Η δημιουργία καινούριων κλάδων και θεωριών (συναρτησιακή ανάλυση, τανυστική ανάλυση, ολική διαφορική γεωμετρία, κυβερνητική, θεωρία γραφημάτων, θεωρία κατηγοριών, θεωρία κατανομών, θεωρία solitons κ.α)
22. Η ανθρωπολογία των μαθηματικών
Αλφαβητικός κατάλογος κυριότερων μαθηματικών.
Σε όποια ονόματα υπάρχει φωτογραφία γίνεται σύνδεση με την Βικιπαίδεια. Κάντε κλικ πάνω στο όνομα και βρείτε βιογραφικά του στοιχεία.
Σε όποια ονόματα υπάρχει φωτογραφία γίνεται σύνδεση με την Βικιπαίδεια. Κάντε κλικ πάνω στο όνομα και βρείτε βιογραφικά του στοιχεία.
Α
Β
Καρλ Βάιστρας (1815-1897) Weierstrass
Γ
Δ
Ε
Πολ Έρντος
Η
Θ
Θέων ο Αλεξανδρεύς
Θεανώ η Θουρία
Θαλής ο ΜιλήσιοςΙ
Κ
Κωνσταντίνος ΚαραθεοδωρήΛ
Άντα Λάβλεϊς
Πιέρ Σιμόν Λαπλάς
Λάιμπνιτς
Λαγκράνζ
Μ
.jpeg/200px-Bernoulli_Nicolaus(II).jpeg&imgrefurl=http://el.wikipedia.org/wiki/%25CE%259D%25CE%25B9%25CE%25BA%25CF%258C%25CE%25BB%25CE%25B1%25CE%25BF%25CF%2585%25CF%2582_%25CE%2592%27_%25CE%259C%25CF%2580%25CE%25B5%25CF%2581%25CE%25BD%25CE%25BF%25CF%258D%25CE%25BB%25CE%25B9&usg=__r6iPOlv8GOrE70HM1_II3tk14ZM=&h=246&w=200&sz=11&hl=el&start=6&zoom=1&itbs=1&tbnid=-G023ZMB_uSiVM:&tbnh=110&tbnw=89&prev=/images%3Fq%3D%25CE%25BC%25CF%2580%25CE%25B5%25CF%2581%25CE%25BD%25CE%25BF%25CF%258D%25CE%25BB%25CE%25B9%26hl%3Del%26gbv%3D2%26tbs%3Disch:1)
Ντάνιελ ΜπερνούλιΝ
- Τζων Φορμπς Νας
Τζον Νέπερ
Τζον φον Νόιμαν
ΝτεκάρτΣαρλ-Εζέν Ντελωναί
Κρίστιαν Ντόπλερ
Ντ΄ Αλαμπέρ
Ο
Π
Πυθαγόρας ο Σάμιος
Μπλεζ Πασκάλ
Ρ
Μπέρναρντ Ρίμαν
Σ
- Εμιλί ντι Σατλέ
- Γιόζεφ Στέφαν
- Ίαν Στιούαρτ
- Σωσιγένης ο Αλεξανδρεύς
Υ
- Υψικλής ο Αλεξανδρος
Φ
Φιμπονάτσι
Ζοζέφ ΦουριέΧ
Κρίστιαν Χόυχενς
Μόσχος Αλέξανδρος του Γρηγορίου;
ΑπάντησηΔιαγραφήToυ Βασιλείου.
ΔιαγραφήΜόλις κυκλοφόρησε το νέο ψηφιακό βιβλίο (ISBN 978-618-84901-2-3) του Δημ. Ν. Κονιδάρη:
ΑπάντησηΔιαγραφή“Ιστορία των θετικών τεχνών και επιστημών κατά την Αρχαιότητα: αποσιώπηση και μεροληψία”
με τον εναλλακτικό τίτλο:
“The history of Mathematics and Exact Sciences in antiquity: Discrimination and aposiopesis”. Το βιβλίο, γραμμένο στην Ελληνική, διατίθεται από την AMAZON κατά δε την περίοδο 12-16.07.2020 θα είναι διαθέσιμο για ΔΩΡΕΑΝ ‘κατέβασμα’ από τον σύνδεσμο:
https://www.amazon.co.uk/Dimitrios-Konidaris/e/B089FJLS5Z/ref=dp_byline_cont_pop_book_1
Τυχόν κριτική ενθαρρύνεται, μπορεί δε να αποσταλεί στο konidaris@ieee.org ή υπό την μορφή σχολίου στο ιστολόγιό μου:
https://www.blogger.com/blog/post/edit/4313881823073841919/7062882291375540026
ή και στην σελίδα της AMAZON.
Χαιρετισμούς
ΔΝΚ